Ⅰ. 서론
전월세전환율은 임대차시장에서 전세보증금을 월세로 전환하는 비율을 의미하는 것으로 전세와 월세 사이의 매개역할을 담당한다 (김상진 외, 2016). 전월세전환율과 시장이자율과의 관계에 대한 이해는 시장이자율에 비해 전월세전환율이 어느 정도의 위험프리미엄을 가지는지, 그리고 시장이자율의 변동으로 전세시장과 월세시장 사이의 불균형이 발생할 수 있으며 이 불균형이 해소되는 데 소요되는 시간에 대한 정보를 파악하는데 도움을 줄 수 있다(이용만 ․ 도경수, 2015). 이로 인해 전월세전환율과 시장이자율 사이의 관계를 이해하는 것이 중요하며, 김상진 외(2016)는 전월세전환율과 시장이자율 사이의 동조화 혹은 조정 과정에 대한 연구가 중요한 이유를 두 가지로 언급하고 있다.
첫째, 전세제도는 은행을 거치지 않고 이루어지는 임대인과 임차인 사이의 직접 금융거래의 형태이기 때문에, 금융시장에서의 시장이자율과 전월세전환율 사이의 관계를 검토하는 것이 중요하다. 둘째, 2008년의 글로벌 금융위기 이후 주택의 기대가격상승률이 하락하고 시장이자율도 하락하였으며, 이로 인해 주택시장에서 주택의 월세화가 진행되었다는 점이다. 시장이자율이 하락하게 되면 임차인의 사용자비용이 하락하게 되고, 이로 인해 전세수요는 상승하게 된다. 이러한 상황에서 전세와 월세 사이의 균형조건을 만족시키기 위해서 전월세전환율이 하락할 수 있다(윤만식 외, 2023).
이와는 달리 이론적 관점에서 시장이자율과 전월세전환율 사이의 관계를 살펴볼 수 있다. 전월세전환율에 대한 이론적 논의는 크게 세 가지로 정리할 수 있다.1) 첫 번째는 자기자본수익률 관점에서 접근하는 이론이다. 이 이론에 의하면 임대인이 주택을 전세로 보유할 때의 자기자본수익률과 월세로 임대할 때의 자기자본수익률은 균형상태에서 같아야 한다. 균형상태에서 차입이자율이 하락하면 임대인의 입장에서 금융비용이 하락하기 때문에 전월세전환율이 하락하게 된다.
두 번째는 전월세전환율을 시장이자율과 위험 프리미엄(risk premium)의 합으로 보는 이론이다. 월세의 경우 임대인에게는 임대 시 공실로 인한 손실위험 그리고 월세 미납 위험이 존재하며, 전세의 경우에는 전세 보증금 회수에 대한 위험이 임차인에게 존재한다. 이러한 임대인과 임차인의 위험으로 인해 전월세전환율에 위험 프리미엄이 반영된다는 이론이다.
세 번째는 임차인의 관점에서의 사용자비용이론2)을 이용하여 접근하는 이론이다. 이 이론에서 전세의 사용자비용은 전세보증금에 시장이자율(혹은 예금이자율, 대출이자율)을 곱한 것이며, 월세의 사용자비용은 전세보증금에 전월세전환율을 곱한 것이다. 균형상태에서는 이 두 가지 사용자비용을 통해 시장이자율이 하락하게 되면, 전세의 사용자비용이 낮아지고, 그로 인해 전월세전환율이 낮아진다.
이러한 세 가지 이론과는 달리 안세륭 외(2020)는 옵션을 이용하여 임대인의 관점에서 무차익 전월세전환율을 도출하였으며, 전월세전환율에 영향을 미칠 수 있는 네 가지 요인(시장이자율, 주택가격 변동성, 월세 프리미엄, 임대 만기)을 검토하였다. 추정결과를 바탕으로 전월세전환율은 시장이자율과 스프레드의 합과 같다는 것을 보여주고 있다.
이상의 연구들은 전월세전환율과 시장이자율 사이의 관계에 대한 검토가 중요하다는 것을 보여준다. 시장이자율과 전월세전환율 사이의 관계에 대해 검토한 대표적인 연구로는 김상진 외(2016), 이용만(2012), 이용만 ․ 도경수(2015), 이창무 외(2009) 등을 들 수 있다. 이창무 외(2009)는 레버리지 가설에 기초하여 분석한 결과, 서울시 아파트 임대시장에서 전월세전환율은 이자율보다는 기대가격상승률과 자본환원율에 의해 결정되는 것으로 나타났다. 이용만(2012)은 전월세시장이 균형관계를 이루기 위해서는 전월세전환율이 시장이자율과 위험프리미엄의 합과 같아야 한다는 이론적 관계를 도출하였다. 이러한 이론적 관점에 대한 실증분석을 통해 시장이자율인 주택담보대출금리와 전월세전환율은 장기적 균형관계를 가진다는 것을 발견하였다. 이용만 ․ 도경수(2015)는 이용만(2012)의 모형을 기반으로 한 오차수정모형(error correction model)을 이용하여 전월세전환율과 시장이자율 대용변수인 국고채 3년 수익률과의 관계를 검토하였으며, 전월세전환율과 국고채 3년 수익률은 장기 균형관계에 있는 것으로 나타났다. 김상진 외(2016)는 ARDL(autoregressive distributed lag) 모형을 통해 서울과 경기 지역에서의 시장이자율(신규 가계대출금리)과 전월세전환율 사이의 동조화를 검토하였다. 이들의 검토 결과는 전월세전환율과 가계대출금리 사이에 장기균형관계가 존재하는 것으로 보고하고 있다.
이러한 선행연구는 시장이자율 변화에 따른 전월세전환율의 조정과정이 대칭적이라는 것을 가정하고 있다. 즉, 시장이자율의 변화와 전월세전환율의 변화는 선형관계를 가지고 있다는 가정 하에 분석하고 있다.
일반적으로 대칭적 조정과정을 가정하는 전통적 모형의 경우 시장 마찰(market frictions), 정보의 비대칭성(asymmetric information) 그리고 거래비용(transaction costs)으로 인해 나타날 수 있는 비대칭적 조정과정을 고려하지 못하는 단점을 가지고 있다(Yuksel, 2016). 부동산시장에서도 취 ․ 등록세, 양도세, 중개수수료, 이사비용 그리고 주택탐색에 소요되는 시간 비용 등 다양한 거래비용3)이 존재한다. 예를 들어, 시장이자율이 하락하면 임대인(임차인)은 전세(월세)를 월세(전세)로 전환하고자 한다. 이로 인해 전세가격이 상승하고 월세가격이 하락하면서 전월세전환율은 하락한다. 이 과정에서 임대인은 전세금을 돌려주어야 하며, 임차인은 차입을 통해 전세금을 지급하여야 한다. 만약, 이 과정에서 임대인(혹은 임차인)이 차입에 대한 제약이 존재하거나 그 비용이 높을 경우, 시장이자율의 변화에 대한 전월세전환율의 조정과정이 차입에 대한 제약이 없거나 차입비용이 낮은 경우에 비해 다르게 나타날 수 있다. 이는 특정한 임계치(threshold)를 기준으로 시장이자율은 전월세전환율에 비대칭적 영향을 미칠 수 있음을 의미한다.
또한, Wang and Lee(2009)는 우리나라 시장이자율(money market rate)에서 예금이자율과 대출이자율로의 이자율 전가(interest rate pass-through)를 검토한 결과, 시장이자율에서 대출이자율로의 이자율 전가에서 비대칭성이 존재한다고 보고하고 있다. 전월세전환율에 대한 세 가지 이론 가운데 자기자본수익률의 관점에서는 차입이자율(즉, 은행의 대출이자율)의 변화는 임대인의 금융비용의 변화를 유발하고, 이는 전월세전환율에 영향을 미친다. 또한, 임차인 관점에서 전월세전환율에 대한 결정이론에서 따르면, 은행 대출이자율의 변화는 전세에서의 사용자비용의 변화를 초래하고 이는 다시 전월세전환율에 영향을 미친다. 즉, Wang and Lee(2009)에서 논의하고 있듯이, 시장이자율의 변화가 은행의 대출이자율에 비대칭적인 영향을 미친다면, 시장이자율의 변화는 전월세전환율에도 비대칭적인 영향을 미칠 수 있다.
본 연구의 목적인 전월세전환율에 대한 시장이자율의 비대칭적 영향을 분석하기 위해, 김상배(2019), 이영수(2022)에서 활용된 Enders and Siklos(2001)의 방법론을 이용하며, 이 방법은 특정한 임계치를 기준으로 장기균형으로의 조정속도에 차이가 있는지를 검토할 수 있는 장점이 있다. 보다 구체적으로 살펴보면, 시장이자율(국고채 3년 수익률 혹은 주택담보대출금리)이 전월세전환율에 미치는 장기적 관점에서의 비대칭적 영향을 분석하기 위해 Enders and Siklos(2001)가 제안한 임계 자기회귀(threshold autoregressive, TAR) 모형과 모멘텀 임계 자기회귀(momentum threshold autoregressive, MTAR) 모형을 이용한 비대칭 임계 공적분(asymmetric threshold cointegration) 방법을 활용하고, TAR 모형과 MTAR 모형 가운데 적절한 모형을 선택한다. 이후 이들 가운데 선택된 모형을 이용하여 비대칭 오차수정(asymmetric error correction) 모형을 설정하고, 이를 추정함으로써 전월세전환율의 단기적 조정과정을 검토하고자 한다. Engle and Granger(1987)의 공적분 검정방법을 보다 일반화한 Enders and Siklos(2001)의 방법론은 공적분과 비대칭성을 동시에 검정할 수 있는 특징이 있다(이영수, 2022). 전월세전환율에 대한 시장이자율의 대칭적 영향을 분석한 기존 연구의 틀을 확장하여 시장이자율의 비대칭적 영향을 검토한다는 점에서 본 연구의 의의가 있다.
본 연구에서 활용하는 국고채 3년 수익률과 주택담보대출금리 그리고 전월세전환율 사이의 비대칭적 관계를 검토하기 위해, 다음과 같은 두 가지 가설을 설정할 수 있을 것이다. 첫 번째 가설은 임대인(혹은 임차인)이 전세금을 지급하기 위해 대출을 받을 경우, 대출에 따른 비용으로 인해 대출이자율의 변화에 대한 전월세전환율의 조정과정이 비대칭적일 수 있다는 것이다. 두 번째 가설로는 Wang and Lee(2009)에서와 같이 국고채 3년 수익률로 대리되는 시장이자율의 변화에 대해 대출이자율이 비대칭적 조정과정을 가질 수 있기 때문에 전월세전환율도 시장이자율에 대해 비대칭적 조정과정을 가질 수 있다는 것이다.4)
이러한 가설과 추정모형을 추정한 결과, TAR 모형과 MTAR 모형을 추정한 결과에서는 선행연구와 유사하게 시장이자율과 전월세전환율 사이에는 장기적 균형관계가 존재하는 것으로 나타났으며, 시장이자율과 전월세전환율 사이의 장기적 관계는 장기균형에서의 이탈의 정도 혹은 이탈 폭의 정도에 따라 균형으로 수렴하는 속도가 다른 것으로 추정되었다. 또한, 비대칭 오차수정모형의 추정결과에서는 국고채 3년 수익률이 전월세전환율에 영향을 미치는 것은 비대칭적 조정과정을 거치지만, 주택담보대출금리는 비대칭적 조정과정을 거치지 않는 것으로 나타났다. 이는 시장수익률의 변화에 따른 대출이자율의 조정과정이 비대칭적이고 이로 인해 전월세전환율도 비대칭적 조정과정을 보이지만, 대출이자율에 대해서는 전월세전환율이 비대칭적인 조정과정을 보이지 않는 것으로 판단된다. 이는 대출비용 때문에 전월세전환율이 비대칭적으로 조정되는 것은 아니라는 것을 의미한다.
본 연구는 다음과 같이 구성되어 있다. 제Ⅰ장의 서론에 이어 제Ⅱ장에서는 본 연구의 실증 분석모형에 대해 구체적으로 살펴보고, 제Ⅲ장에서는 표본자료 및 실증분석 결과를 제시한다. 마지막으로 제Ⅳ장에서는 분석결과의 요약과 결론을 제시한다.
Ⅱ. 실증 분석모형
시장이자율의 변화는 전월세시장의 변화를 유발하고, 이는 다시 전월세전환율을 변화시킨다(이용만 ․ 도경수, 2015). 하지만, 임대인(임차인)의 차입에 따른 차입비용 등의 존재로 인해 시장이자율의 변화가 전월세전환율의 변화에 비대칭적 영향을 미칠 수 있다. 이를 검정하기 위해 TAR 모형 혹은 MTAR 모형을 활용한 비대칭 오차수정모형을 활용한다.
이용만(2012), 이용만 ․ 도경수(2015)에서 볼 수 있듯이, 전세시장과 월세시장의 동시적 균형조건은 다음과 같이 표현할 수 있다.
여기서, R/C는 전월세전환율을 나타낸다. s+π는 위험프리미엄을 나타내며, 이는 관찰이 불가능하다. 무위험자산의 수익률인 i 역시 관찰이 불가능하지만, 일반적으로 시장이자율인 국고채 수익률을 사용한다. 시장이자율(rt)과 전월세전환율 사이의 장기적 균형관계는 (식 1)을 활용하여 다음과 같이 표현할 수 있다(이용만, 2012; 이용만 ․ 도경수, 2015).
전월세전환율과 시장이자율이 단위근을 가지는 불안정 시계열이라면, (식 2)는 공적분 함수라고 할 수 있고, 이 때 et는 장기균형에서의 이탈 정도를 나타내는 오차수정항(error correction term)이 된다. 이 오차수정항은 회귀분석을 통해 추정이 가능하다. 하지만, 본 연구에서는 단위근(unit root)을 가지는 독립변수의 선 ․ 후행 차분변수를 설명변수로 추가함으로써 독립변수들 사이에서 존재할 수 있는 연립편차(simultaneity bias)를 고려할 수 있고(장병기, 2011) Stock and Watson (1993)이 제안한 동태적 회귀분석(dynamic ordinary least square, DOLS) 모형을 이용하여 두 변수 사이의 장기적 관계를 검토한다.
여기서, ɛt는 DOLS 모형을 통해 추정된 잔차(residuals)를 나타낸다. (식 3)의 DOLS에서 도출한 오차수정항(ɛt)을 이용하여 시장이자율과 전월세전환율 사이의 관계는 다음과 같은 오차수정모형으로 표현이 가능하다.
(식 4)에서 ɛt-1은 전기의 전월세전환율이 시장이자율로부터 이탈한 정도를 나타내고, 전월세전환율과 시장이자율 사이의 장기균형관계로 수렴하기 위해서는 γ가 유의한 음(‒)의 값을 가져야 한다.
(식 4)에 제시된 오차수정모형은 장기균형에서의 이탈이 미치는 영향이 대칭적이라는 것을 전제로 하고 있다. 비대칭성을 고려하기 위해 Enders and Siklos(2001)의 방법과 (식 3)에서 추정한 잔차를 이용하여 TAR 모형 혹은 MTAR 모형을 다음과 같이 표현할 수 있다.
여기서, It는 지시함수(indicator function)를 의미한다. 임계치(threshold value)를 τ라고 할 때 TAR(MTAR) 모형에서는 εt-1 ≥ τ (Δεt-1 ≥ τ)의 관계가 성립하면, It는 1의 값을 가지고 아니면 0의 값을 가진다. 본 연구에서는 이양섭(2008)에서와 같이 Chan(1993)의 방법을 활용하여 임계치 τ를 추정한다. 그 과정을 간략하게 살펴보면, (식 3)을 통해 추정한 잔차를 그 크기에 따라 차례로 나열하여 상하 15%에 해당하는 잔차들을 제거하고, 나머지 70%의 잔차를 이용하여 잔차 제곱합(residual sum of square)을 계산한다. 계산된 잔차 제곱합을 최소화하는 잔차의 값을 임계치로 이용한다.
(식 5)에 나타나 있듯이, TAR 모형(혹은 MTAR 모형)의 경우 εt 〉 τ (Δεt 〉 τ)일 때 장기균형으로의 이탈 정도에 따른 조정과정은 Itρ+에 의해 추정된다. εt 〉 τ 이라는 것은 시장이자율과 전월세전환율의 괴리가 특정한 임계치보다 크다는 것을 의미하며, Δεt 〉 τ 는 시장이자율과 전월세전환율 사이의 괴리의 폭이 특정한 임계치보다 크다는 것을 의미한다. 달리 표현하면, 시장이자율과 전월세전환율 사이의 괴리(괴리폭)가 임계치보다 큰 경우는 ρ+의 속도로 불균형을 조정하고, 괴리(괴리폭)가 임계치를 초과하지 않으면 ρ-의 속도로 조정하다는 것을 의미한다. 예를 들어 τ=0인 경우를 살펴보면, εt가 임계치보다 크다는 것은 시장이자율(전월세전환율)이 전월세전환율(시장이자율)보다 상대적으로 많이 하락(상승)함으로써 시장이자율과 전월세전환율 간의 차이(spread)가 확대되었다는 것을 의미한다. 이 때 시장이자율에 비해 전월세전환율이 상대적으로 많이 하락하게 되면 장기균형으로 회복할 수 있을 것이다. 이에 비해 εt 〈 τ(Δεt 〈 τ)일 경우에는 상대적으로 전월세전환율이 상승함으로써 장기균형을 회복할 수 있다. 하지만, 장기균형으로부터 이탈이 발생하고 그 정도가 임계치보다 크거나 작은 경우 장기균형으로 다시 회복하는 과정에서 차이가 나타날 수 있다. 이러한 장기균형으로의 회복 과정에서의 차이는 (식 5)에서 나타난 추정계수 ρ+와 ρ-에 의해 측정된다.
또한, (식 5)의 추정결과를 이용하여 공적분 관계 그리고 장기균형으로 조정 과정에서 나타날 수 있는 비대칭성을 검정할 수 있다. 공적분 관계는 (식 5)에서 ρ+=ρ-=0의 관계가 성립하는지를 통해 알 수 있는데, 이 관계가 기각되면 전월세전환율과 시장이자율 간에는 공적분 관계가 존재한다는 것을 의미한다. 또한, 장기적 대칭성의 성립여부는 ρ+ = ρ-의 관계를 검토함으로써 알 수 있으며, 이 관계가 기각되면 장기균형으로의 조정과정에서 비대칭성이 존재한다(이영수, 2022)는 것을 의미한다. 즉, 가설 ρ+=ρ-이 기각된다면, 이는 양(+)의 편차와 음(‒)의 편차에 따른 장기균형으로의 수렴과정이 서로 유의하게 차이가 있음을 나타낸다.
이러한 TAR 모형 혹은 MTAR 모형의 추정결과를 (식 3)의 오차수정항 대신 대입하면 다음과 같은 비선형 오차수정모형을 얻을 수 있으며, 이 모형은 전월세전환율이 장기균형에서의 이탈로부터 발생한 오차를 단기적으로 조정해 나가는 과정을 나타낸다.
(식 6)에서 시장이자율의 변화가 전월세전환율의 변화에 단기적으로 미치는 영향은 β1을 통해 추정할 수 있으며, 장기균형에서의 이탈이 전월세전환율의 변화에 미치는 단기적인 영향은 추정계수 δ+와 δ-의 유의성을 통해 판단할 수 있다.
Hiemstra and Jones(1994)에 의하면 변동성 효과로 인해 주식수익률과 같은 자산가격 변화율에서의 비선형성이 나타날 수 있다. 또한, Wang and Lee(2009)는 (식 6)과 같이 이분산성(heteroskedasticity)을 고려하지 않고 비대칭 오차수정모형을 추정할 경우 편의된 추정치가 나타날 가능성이 있다고 한다. 이러한 점을 감안하여 본 연구에서는 Wang and Lee(2009)와 같이 (식 6)에 조건부 표준편차를 추가한 (식 7)을 평균방정식으로 하고, (식 8)에 제시된 GARCH(1,1) 모형을 분산방정식으로 하는 EC-GARCH(1,1)-M 모형을 추가로 검토하고자 한다.
여기서, 은 (식 7)에 나타난 잔차(ut)의 조건부 분산(conditional variance)을 나타낸다.
Ⅲ. 표본자료 및 실증분석 결과
아파트는 표준화된 특성을 가지고 있고 대체성과 거래량이 많아 주택가격이 비교적 효율적으로 결정될 가능성이 높기 때문에(윤만식 외, 2023), 본 연구에서는 한국 부동산원에서 제공하는 월별 전국 아파트 전월세전환율을 활용하며, 이 전월세전환율은 전월세 확정일자 신고를 바탕으로 구축된 자료이다(황관석, 2018). 시장이자율로는 한국은행에서 제공하는 국고채 3년 수익률과 신규취급액 기준 주택담보대출금리5)를 활용하며, 한국부동산원에서 전월세전환율을 2011년 1월부터 제공하기 때문에 표본 기간은 2011년 1월부터 2023년 8월까지이다.
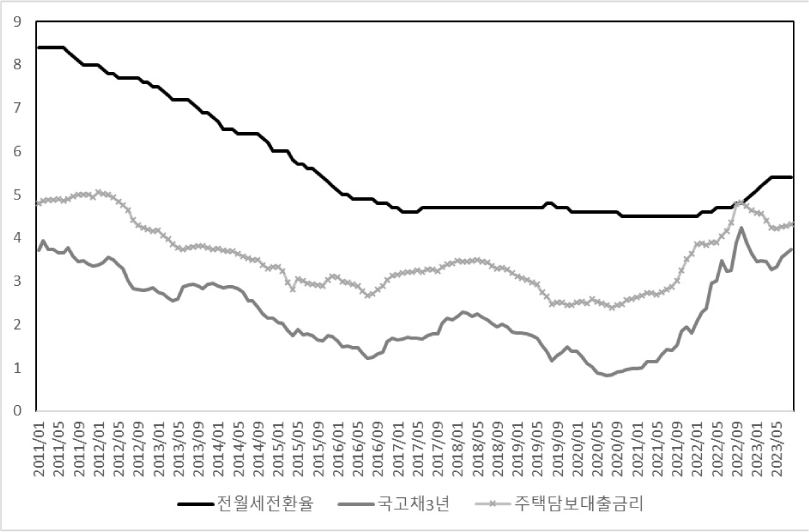
<그림 1>에서는 표본 기간 동안의 전월세전환율, 국고채 3년 수익률 그리고 주택담보대출금리의 추이를 보여주고 있다. 국고채 3년 수익률과 주택담보대출금리는 2020년 8월까지는 서서히 하락하는 흐름을 보이다가, 코로나19 이후 미국의 금리상승 기조에 따라 우리나라의 이자율 역시 2020년 후반기부터 상승하는 흐름을 보여주고 있다. 전월세전환율의 경우 2022년 2월부터 상승하고 있다는 것을 보여주고 있다. 또한, <그림 1>에서는 황관석(2018)에서 논의하듯이, 전반적으로는 전월세전환율은 시장이자율보다 높은 수준에 있다는 것을 보여주고 있다.
(식 2)와 (식 3)에서 볼 수 있듯이, 두 시계열 변수 사이에 장기적 관계가 존재하기 위해서 두 변수는 각각 단위근(unit root)을 가지고 있는 불안정한 시계열이어야 한다. 본 연구에서는 전월세전환율, 국고채 3년 수익률 그리고 주택담보대출금리에 대한 단위근 검정을 실시하였으며, 그 결과는 <표 1>의 Panel A에 제시되어 있다. 표에서 수준변수는 전월세전환율, 국고채 3년 수익률 그리고 주택담보대출금리를 나타내며, 차분변수는 수준변수를 1차 차분한 것이다. 본 연구에서는 단위근 검정을 위해 전통적인 방법인 ADF 검정과 PP 검정을 활용하였으며, 각 검정방법에서 상수항만 포함한 경우와 상수항과 추세(linear trend)를 포함한 경우로 구분하여 추정하였다. 추정 결과를 살펴보면, 상수항만을 포함한 PP 검정에서 전월세전환율을 제외한 다른 모든 수준변수에서는 단위근이 존재한다는 것을 보여주고 있으며, 차분변수는 모두 단위근을 가지고 있지 않는 것으로 나타났다. 추가적으로 본 연구에서는 전월세전환율에 대해 ERS(Elliot, Rotherberg, Stock Point Optimal) 검정과 KPSS(Kwiatkowski–Phillips-Schmidt–Shi) 검정을 실시하였다. ERS 검정은 시계열 자료가 단위근을 가지고 있다는 귀무가설을 검토하며, KPSS 검정은 단위근을 가지고 있지 않다는 귀무가설을 검정한다. 추정결과, ERS 검정통계량은 ‒1.038(5% 수준의 임계치 ‒1.943), KPSS 검정통계량은 0.354(5% 수준의 임계치 0.463)로 나타났으며, 이들 결과는 전월세전환율은 단위근을 가지고 있는 것으로 나타났다.6) 이러한 결과를 바탕으로 전월세전환율, 국고채 3년 수익률 그리고 주택담보대출금리는 모두 수준변수에서는 단위근이 존재하고, 1차 차분변수에서는 단위근이 존재하지 않는, 안정적(stationary)인 변수라고 판단하고 추후의 분석을 진행하고자 한다.
시장이자율과 전월세전환율이 모두 수준변수에서 단위근을 가지고 있기 때문에, 두 변수 사이에 공적분관계가 존재할 수 있다. 이를 검정하기 위해 Johansen 공적분 검정을 실시하였으며 그 결과는 <표 1>의 Panel B에 제시되어 있다. 추정결과, 전월세전환율과 국고채 3년 수익률 사이, 그리고 전월세전환율과 주택담보대출금리 사이에는 한 개의 공적분 관계가 존재하는 것으로 나타났다.
김윤영 ․ 박준용(2007)에 의하면, Johansen 공적분 검정은 Engle-Granger 검정과 같은 잔차기준 검정법에 비해 공적분 관계의 존재를 기각하지 않는 성향이 있다. 이러한 특성으로 인해 김윤영 ․ 박준용(2007)은 Johansen 검정과 같이 VAR 모형을 이용하는 공적분 검정을 실시할 때 공적분 후보 벡터로부터 정의되는 오차에 대해 단위근을 검정할 것을 제안하고 있다. 이에 본 연구에서는 <표 1>의 Panel B에서의 추정과정에서 도출된 공적분 벡터로부터 정의되는 오차에 대한 단위근을 검정하였으며, 그 결과는 <표 2>에 제시되어 있다.
| ADF | PP | |||
|---|---|---|---|---|
| 상수항 | 상수항+추세 | 상수항 | 상수항+추세 | |
| 국고채 3년 수익률 | -0.714 | -2.190 | -0.829 | -2.094 |
| (0.839) | (0.491) | (0.808) | (0.544) | |
| 주택담보대출금리 | -1.438 | -2.540 | -1.317 | -2.204 |
| (0.562) | (0.309) | (0.621) | (0.484) | |
<표 2>에 제시된 추정결과는 두 가지 공적분 벡터로부터 정의된 오차에서 단위근이 존재한다는 것을 보여주고 있으며, 이는 표준적인 공적분 접근방법에서 나타나는 회귀모형 오차의 안정성 조건을 만족하지 못한다는 것으로 공적분 관계가 존재하지 않는 것을 의미한다. 이는 김윤영 ․ 박준용(2007)에서 주장하듯이 Engle-Granger 검정과 같은 잔차기준 검정법에 비해 Johansen 검정 방법은 공적분 관계의 존재를 기각하지 않는 성향이 있기 때문인 것으로 판단된다.
<표 3>에서는 전월세전환율과 시장이자율에 대한 요약통계량이 제시되어 있다. <표 3>에서 제시된 세 가지 변수의 평균에서 볼 수 있듯이 전월세전환율은 평균적으로 국고채 3년 수익률과 주택담보대출금리보다 높은 수준을 유지하고 있음을 보여주고 있다.
표준편차를 비교해 보았을 때, 표본 기간 동안 국고채 3년 수익률의 변동성이 가장 높은 것으로 나타났다. 세 가지 변수 모두에서 왜도는 양(+)의 값을 가지는 것으로 추정되었으며, 세 가지 변수 모두 각각의 분포에서 오른쪽 꼬리 부분이 두텁다는 것을 의미한다. 마지막으로 Jarque-Bera 통계량은 세 가지 변수 모두가 정규분포를 따르지 않는 것을 보여주고 있다.
Johansen 공적분 검정방법은 대칭성을 가정하고 있으며, 시계열 자료에서 발생할 수 있는 구조적 변화(structural break)를 고려하지 못하는 단점이 있다. 표본 기간 동안 구조적 변화가 존재하는지에 대해 검토하기 위해 Bai and Perron (2003)의 검정방법을 이용하여 구조적 변화의 존재 여부를 추정하였으며, 그 결과는 <표 4>에 제시되어 있다.
추정결과를 요약하면, 표본 기간 동안 전월세전환율과 국고채 3년 수익률 사이에는 2번의 구조적 변화(2013년 8월과 2016년 10월)가 발생한 것으로 나타났으며, 전월세전환율과 주택담보대출금리 사이에는 2013년 9월, 2015년 12월 그리고 2019년 12월에 구조적 변화가 있는 것으로 나타났다.7)
<표 4>의 추정결과는 공적분검정에 있어 구조적 변화를 고려할 필요가 있다는 것을 의미한다. 이를 반영하기 위해 본 연구에서는 McLeod and Haughton(2018)에서와 같이 구조적 변화를 반영하는 더미변수를 DOLS 모형에 반영하여 구조적 변화를 고려한 잔차를 도출하고, 이를 이용하여 공적분 검정을 실시하였다. 추정결과는 <표 5>에 제시되어 있다. 추정과정에서 국고채 3년 수익률과 전월세전환율 사이의 관계를 검토할 때는 구조적 변화가 발생한 두 가지 시기에 시간더미변수(시간더미 1과 시간더미 2로 표시)를 추가하였으며, 이들 더미변수는 모두 유의한 것으로 나타났다. 하지만, 전월세전환율과 주택담보대출금리와의 관계를 검토할 때 사용된 2015년 12월 그리고 2019년 12월에 해당하는 시간더미는 유의하지 않은 것으로 나타나, 이들 더미변수를 제외한 DOLS 모형 추정결과를 <표 5>에 제시하고 있다.8)
<표 5>에 제시된 추정결과를 살펴보면, 시장이자율이 전월세전환율에 미치는 영향을 나타내는 계수에 대한 추정치는 0.472(국고채 3년 수익률)과 1.803(주택담보대출금리)이고 모두 1% 수준에서 유의한 것으로 나타났다. 이는 김상진 외(2016)와 이용만 ․ 도경수(2015)에서의 결과와 같이 시장이자율과 전월세전환율은 서로 양(+)의 장기균형관계를 가지고 있다는 것을 의미한다. 이는 서론에서 소개한 세 가지 이론에서의 내용과 부합하는 결과이다. 또한, DOLS 모형의 추정결과를 이용한 Engle-Granger 공적분 검정에서는 국고채 3년 수익률은 전월세전환율과 공적분 관계를 가지고 있는 것으로 나타났으며, 이는 전월세전환율과 시장이자율 사이의 공적분 관계가 존재한다는 이용만 ․ 도경수(2015)의 결과와 일치한다. 하지만, 주택담보대출금리와 전월세전환율은 공적분 관계가 존재하지 않는 것으로 추정되었다.
Johansen 공적분 검정과 Engle-Granger 공적분 검정은 모두 오차의 수정과정이 대칭적으로 이루어진다고 가정하고 있다, 하지만, 임대인과 임차인의 차입에 따른 차입비용 등의 존재로 인해 균형으로의 조정과정이 비대칭성을 가질 수 있다. 본 연구에서는 불특정의 임계치(τ)에 따라 공적분 잔차의 비대칭적 조정과정을 반영하는 Enders and Siklos(2001)의 임계 공적분방법(정수관 ․ 원두환, 2020)을 이용하고자 한다. 장기균형으로의 조정 과정에서 비대칭성이 존재하는지를 검토하기 위해 (식 5)에 제시된 TAR 모형과 MTAR 모형을 추정하였으며, 그 결과는 <표 6>에 제시되어 있다.
먼저, 시장이자율과 전월세전환율 사이의 공적분 관계가 존재하지 않는다는 귀무가설(ρ+ = ρ- = 0)의 경우, 국고채 3년 수익률과 주택담보대출금리는 TAR 모형과 MTAR 모형 모두 5% 수준에서 기각할 수 있는 것으로 나타났다. 이는 시장이자율과 전월세전환율 사이에는 공적분 관계가 존재한다는 것을 의미한다. DOLS 검정에서 나타난 결과와 비교하면, 국고채 3년 수익률의 경우는 일치하지만 주택담보대출금리와는 일치하지 않는 결과이다.
F-equal 통계량은 장기균형으로의 조정과정에서의 비대칭성이 존재하는지를 검정하기 위한 것으로, 국고채 3년 수익률의 경우 TAR 모형과 MTAR 모형에서는 각각 5%와 1% 유의수준에서 유의한 것으로 나타나 TAR 모형과 MTAR 모형에서는 장기균형으로의 조정과정이 비대칭적이라는 것을 보여준다. 하지만, 주택담보대출금리의 경우 TAR 모형에서는 유의하지 않고, MTAR 모형에서는 유의한 것으로 나타났다. 이러한 결과는 시장이자율과 전월세전환율 사이에는 장기균형관계가 존재하지만, 충격이 발생하여 장기균형에서 이탈하였을 때 오차가 균형으로 조정하는 과정은 비대칭적이라는 것을 의미한다.
<표 6>에 제시된 국고채 3년 수익률을 활용한 추정결과를 보다 구체적으로 살펴보면, TAR 모형과 MTAR 모형에서의 임계치(τ)는 각각 ‒0.205와 0.066으로 추정되었다. 또한, 공적분의 비대칭과 관련된 변수인 ρ+와 ρ-의 추정결과는 TAR 모형의 경우 ρ-만 유의한 음(‒)의 값을 가지는 것으로 나타났으며, MTAR 모형의 경우 ρ+만 유의한 음(‒)의 값을 가지는 것으로 추정되었다. 이러한 결과는 TAR 모형(MTAR 모형)의 경우 국고채 3년 수익률과 전월세전환율의 괴리(괴리의 폭)가 임계치보다 작을 때(클 때), 장기균형으로의 조정이 발생한다는 것이다. 이러한 결과는 이영수(2022)와 유사하게 공적분 잔차의 변동 방향과 크기에 따라 공적분의 여부가 다르다는 것을 의미한다.
또한, 주택담보대출금리를 이용한 경우에서는 TAR 모형과 MTAR 모형 모두 ρ+와 ρ-가 유의한 음(‒)의 값을 가지는 것으로 추정되었으나, 장기균형으로의 조정속도에서는 TAR 모형의 경우는 주택담보대출과 전월세전환율의 괴리의 정도가 임계치보다 클 때 더 빠르게 조정되고, MTAR 모형에서는 주택담보대출과 전월세전환율 사이의 괴리의 폭이 임계치보다 작을 때 더 빠르게 조정되는 것으로 나타났다. 이러한 결과는 주택담보대출금리와 전월세전환율 사이의 장기적 관계는 괴리의 정도 혹은 괴리의 폭의 정도에 따라 균형으로 수렴하는 속도가 다르다는 것을 의미한다.
TAR 모형과 MTAR 모형 가운데 더 적절한 모형을 판단하기 위해 본 연구에서는 AIC(Akaike information criterion)와 SBC 값을 추정하였다. 추정결과, 두 기준 모두에서 TAR 모형보다 MTAR 모형이 더 적절한 것으로 나타났다. 이러한 두 가지 통계량(AIC와 SBC)에 대한 결과는 장기균형으로의 비대칭 조정과정을 검정할 때 MTAR 모형이 TAR 모형보다 우월하다고 주장하는 Bohl and Siklos(2004)의 주장과 일치하는 결과이다.
<표 6>에서 나타난 것과 같이 시장이자율과 전월세전환율 사이에 장기적 균형관계가 존재한다면, 전월세전환율이 장기균형관계로부터 이탈하였을 때, 이러한 이탈을 조정하여 균형관계로 수렴하여야 한다. 즉, <표 6>에 나타난 비대칭적 공적분검정의 결과는 전월세전환율과 시장이자율 사이에 공적분 관계가 존재한다는 것을 의미한다. 본 연구에서는 다른 공적분 관계를 검토한 선행연구에서와 같이, 비대칭적 공적분 관계를 이용하여 (식 6)에 제시된 비대칭적 오차수정모형을 추정함으로써 전월세전환율의 단기적 조정과정을 검토하고자 한다. 본 연구에서는 MTAR 모형에서 나타난 공적분관계를 이용하여 (식 6)의 비대칭 오차수정모형을 추정하였으며, 그 결과는 <표 7>에 제시되어 있다.
먼저, 시장이자율의 변화가 전월세전환율의 변화에 미치는 단기적 영향은 β1에 의해 측정된다. 추정결과에서 국고채 3년 수익률과 주택담보대출금리 모두에서 β1은 유의하지 않은 것으로 나타났으며, 이는 시장이자율의 변화는 전월세전환율의 변화에 단기적 영향을 미치지 않는다는 것을 의미한다. 이러한 추정결과는 이용만 ․ 도경수(2015)의 추정결과와 유사하다. 이들의 연구에서는 국고채 3년 수익률을 시장이자율의 대용치로 활용하여 시장이자율에 대한 전월세전환율의 조정과정을 검토하였으며, 2001년부터 2008년까지는 시장이자율의 변화가 전월세전환율의 변화에 영향을 미치고 있으나, 2009년 이후의 자료에서는 시장이자율의 변화가 전월세전환율의 변화에 영향을 미치지 않는 것을 발견하였다.
첫 번째 Wald 검정(δ+ = δ- =0)의 결과는 국고채 3년 수익률에서만 1% 유의수준에서 기각할 수 있는 것으로 나타났으며, 두 번째 Wald 검정은 대칭성(δ+ = δ-)을 검정하는 것으로 국고채 3년 수익률에서만 5% 수준에서 유의한 것으로 나타났다. 또한, 국고채 3년 수익률에서의 δ+는 ‒0.113으로, δ-는 ‒0.041로 추정되었다. 이것은 국고채 3년 수익률의 경우 전월세전환율의 차분 시계열은 공적분 잔차의 변동의 크기(Δεt-1)가 임계값(τ=0.066)보다 클 때가 작을 때보다 더 빠르게 전월세전환율을 수정한다는 것이며, 이 공적분 잔차 변동의 크기가 클수록 그 조정속도가 더 빠르다는 것을 의미한다. 즉, 국고채 3년 수익률과 전월세전환율 사이의 괴리의 폭이 클수록 차입비용을 상쇄할 수 있다고 느끼는 시장에서 거래참여자가 증가하고, 그로 인해 전월세전환율의 조정속도가 더 빨라진다는 것으로 판단된다.
요약하면, 국고채 3년 수익률이 전월세전환율에 미치는 영향은 비대칭적 조정과정을 거치지만, 주택담보대출금리는 국고채 3년 수익률과는 다르게 비대칭적 조정과정을 보이지 않는다는 것이다. 이는 시장수익률의 변화에 따른 대출이자율의 조정과정이 비대칭적이고, 이로 인해 전월세전환율도 비대칭적 조정과정을 보이지만, 대출이자율에 대해서는 전월세전환율이 비대칭적인 조정과정을 보이지 않는 것으로 판단된다. 이는 대출비용 때문에 전월세전환율이 비대칭적으로 조정되는 것은 아니라는 것을 의미한다.9)
본 연구에서 활용하고 있는 비대칭 오차수정모형의 경우, 오차수정모형의 잔차에서 존재할 수 있는 이분산성으로 인해 편의된 추정치가 나타날 가능성이 있다(Wang and Lee, 2009). 본 연구에서는 잔차의 이분산성을 고려하기 위해 (식 7)과 (식 8)에 제시된 EC-GARCH(1,1)-M 모형을 추정하였으며, 그 결과는 <표 8>에 제시되어 있다.
평균방정식의 추정결과를 살펴보면, <표 7>의 추정결과와 유사하다는 것을 알 수 있다. 또한, 분산방정식의 추정결과를 통해 전월세전환율의 조건부 분산은 지속성이 높다는 것을 알 수 있다. EC-GARCH-M 모형을 통해 추정된 표준화된 잔차와 표준화된 잔차의 제곱에 대한 Ljung-Box Q 통계량인 LB(8)과 LB2(8)은 모두 유의하지 않은 것으로 나타났다. 이는 표준화된 잔차와 표준화된 잔차의 제곱에서 유의한 시계열 자기상관이 존재하지 않는다는 것으로, 본 연구에서 활용한 EC-GARCH-M 모형이 적절하다는 것을 의미한다. 이러한 결과는 <표 7>의 추정결과는 이분산성을 고려한 상황에서도 강건하다는 것을 의미한다.
Ⅳ. 요약 및 결론
시장 마찰, 정보의 비대칭성 그리고 거래비용 등으로 인해 부동산 가격을 포함한 경제변수는 균형상태에서 이탈하였을 때 이론적 관점에서의 대칭적 조정과정보다는 비대칭적 조정과정이 나타날 수 있다.
시장이자율과 전월세전환율 사이에 비대칭적 조정과정이 존재하는지를 검정하기 위해 본 연구에서는 Enders and Siklos(2001)가 제안한 비대칭 공적분모형과 비대칭 오차수정모형을 활용하였다. 또한, Wang and Lee(2009)의 주장과 같이 이분산성으로 인한 편의된 추정치가 나타날 가능성을 고려하여 EC-GARCH(1,1)-M 모형을 활용하여 강건성을 검정하였다. 본 연구에서는 시장이자율로 국고채 3년 수익률과 신규취급액 기준의 주택담보대출금리를 활용하고, 표본 기간은 2011년 1월부터 2023년 8월까지이다. 추정결과를 요약하면 다음과 같다.
첫째, Johansen 공적분 검정에서는 시장이자율과 전월세전환율 사이의 공적분관계가 존재하지 않는 것으로 나타났으며, DOLS의 잔차를 이용한 검정결과에서는 국고채 3년 수익률과 전월세전환율은 공적분 관계가 존재하지만, 주택담보대출금리에서는 존재하지 않는 것으로 나타났다. 하지만, Enders and Siklos(2001)의 비대칭 임계 공적분 방법에서는 국고채 3년 수익률과 주택담보대출금리 모두 전월세전환율과 공적분 관계가 존재하는 것으로 나타났다. 이러한 차이는 전통적인 공적분 검정방법은 대칭적 조정과정을 가정하기 때문인 것으로 판단된다.
둘째, TAR 모형과 MTAR 모형을 추정한 결과에서는 국고채 3년 수익률의 경우 TAR 모형(MTAR 모형)의 경우 국고채 3년 수익률과 전월세전환율의 괴리(괴리의 폭)가 임계치보다 작을 때(클 때), 장기균형으로의 조정이 발생한다는 것으로 나타났다. 또한, 주택담보대출금리의 경우에서는 장기균형으로의 조정속도측면에서 TAR 모형의 경우는 주택담보대출과 전월세전환율의 괴리의 정도가 임계치보다 클 때 더 빠르게 조정되고, MTAR 모형에서는 주택담보대출과 전월세전환율 사이의 괴리의 폭이 임계치보다 작을 때 더 빠르게 조정되는 것으로 나타났다. 이러한 결과는 시장이자율과 전월세전환율 사이의 장기적 관계는 괴리의 정도 혹은 괴리의 폭의 정도에 따라 균형으로 수렴하는 속도가 다르다는 것을 의미한다.
셋째, MTAR 모형의 추정결과를 이용하여 전월세전환율의 변화에 대한 비대칭 오차수정모형을 추정한 결과, 국고채 3년 수익률이 전월세전환율에 단기적으로 영향을 미치는 것은 비대칭적 조정과정을 거치지만, 대출금리는 국고채 3년 수익률과는 다르게 비대칭적 조정과정을 보이지 않는다는 것이다. 이는 시장수익률의 변화에 따른 대출이자율의 조정과정이 비대칭적이고 이로 인해 전월세전환율도 비대칭적 조정과정을 보이지만, 대출이자율에 대해서는 전월세전환율이 비대칭적인 조정과정을 보이지 않는 것으로 판단된다. 이는 대출비용 때문에 전월세전환율이 비대칭적으로 조정되는 것은 아니라는 것을 의미한다.
시장이자율과 전월세전환율 사이의 공적분 관계가 존재한다는 것은 충격에 의해 일시적으로 불균형이 발생하더라도 시간이 지나면 장기균형관계로 회복된다는 것을 의미한다. 하지만, 실제 부동산 거래에서 발생하는 차입비용의 존재 등으로 인해 시장이자율과 전월세전환율 사이에는 비대칭적 조정과정이 나타날 수 있다. 이는 시장이자율 충격에 의해 일시적으로 전월세시장 사이에 불균형이 발생할 때, 장기균형으로부터의 이탈의 방향과 속도에 따라 균형상태로의 조정과정이 다르다는 것을 의미한다. 본 연구의 목적인 시장이자율과 전월세전환율 사이의 비대칭적 관계를 검토하는 것은 전월세시장이 균형상태에서 이탈하였을 때, 새로운 균형으로의 회복과정을 이해하는 데 도움을 줄 것이다. 이러한 전월세시장에 대한 이해를 바탕으로, 정책당국에서는 부동산시장에 대한 정책을 수립할 때 시장이자율의 변동의 방향과 속도에 대해서도 주의 깊게 살펴보아야 한다는 것을 의미한다.
본 연구는 전국을 대상으로 산출한 전월세전환율과 시장이자율 사이의 관계를 분석하는 한계점을 가지고 있다. 윤만식 외(2023)에 의하면, 전월세전환율에 영향을 미치는 요인은 다양하며, 지역별로 차이가 있다. 추후 연구에서는 구체적으로 어떠한 요인들이 전월세전환율과 시장이자율 사이의 비대칭적 조정과정에 영향을 미치는지를 검토할 필요가 있다. 또한, 지역별로 시장이자율과 전월세전환율 사이의 장단기 관계를 검토하는 것은 지역별 부동산 시장을 이해하는 데 도움을 줄 수 있을 것으로 생각된다. 또한, 현재의 연구는 2011년 이후의 자료를 활용하고 있어, 비교적 짧은 표본 기간을 사용함으로 인해 경기 변동에 따른 효과를 검토하지 못하였다는 점을 추가적인 한계점으로 들 수 있다. 이러한 점들은 추후 연구과제로 남겨둔다.