Ⅰ. 서론
국내 주택 임대차 시장에서 월세의 비중이 점차 증가함에 따라, 이에 대한 시장 모니터링과 정책 대응의 중요성이 커지고 있다. 임대료 변동은 도시민의 주거 수준에 중대한 영향을 미치며, 소비자와 기업의 의사결정뿐 아니라 정부의 경제정책 수립에도 중요한 요소로 작용하므로 이에 대한 정확한 평가가 요구된다.
한국의 월세 시장은 보증금과 월세의 다양한 배율 관계에 따라 하부시장이 형성된다. 월세 보증금은 임대인의 입장에서 잠재적인 수익을 발생시킬 수 있는 기회비용을 내포하고 있어 사실상 임대료의 기능을 일부 수행하게 된다. 이처럼 상당한 수준의 보증금이 임대료의 일부 기능을 수행하는 현상은 한국뿐만 아니라 볼리비아, 인도, 이란 등의 국가에서도 관찰되며, 이에 따라 보증금의 기회비용을 반영한 정교한 임대료 산정 방식이 요구된다(Kim, 2024; UN-Habitat, 2003).
현재 국내 대표적인 월세 지수로는 한국부동산원의 전국주택가격동향조사 내 월세지수, KB국민은행이 작성·발표하는 KB월세지수, 그리고 소비자물가지수를 구성하는 집세지수(월세지수)가 있으며 모두 조사·평가 가격에 기반한 지수이다. 조사·평가 가격에 기반한 가격지수가 가진 여러 한계를 보완하기 위해 한국부동산원은 국가 공식 통계 작성 기관으로서 실거래가격에 기반한 매매지수와 전세지수를 각각 2006년과 2014년부터 작성·발표해왔다. 그러나 월세가격지수의 경우, 실거래가격에 기반한 지수 구축이 여러 가지 제약 사항으로 인해 지연되고 있다. 보증금과 월세의 배율 관계에 따른 정확한 전월세전환율을 산정이 어려운 점, 주택 표본의 일관성을 확보하기 어렵다는 점 등이 주요한 원인으로 제시된다.
본 연구에서 제안하는 기계학습 기반 지수는 지수 자체를 직접 추정하거나 예측한 기존 선행연구와 달리, 관측 기간과 지역의 아파트를 구성하는 개별 세대의 잠재가격을 추정한 뒤, 각 주택의 가격에 해당 세대 수를 가중치로 곱하여 시점별 총 자산가치 변동을 계산하는 방식을 적용한다. 이를 통해 개별 단지, 행정동, 또는 특정 면적 조건 등을 만족하는 단지를 선별하여 작성할 수 있는 유연성과 확장성이 확보되므로 기존 지수보다 시공간적 해상도가 정밀한 산정이 가능하다.
본 연구는 월세지수 산정 방식에 관한 선행연구와 실거래가 기반의 중위값 추이를 검토한 후 반복매매지수와 기계학습 기반 지수를 산정한다. 아울러 타 기관이 작성한 지수와의 비교를 통해, 기존 방법론이 갖는 주요 제약인 거래 공백 기간과 소지역 단위 가격 추정 시 표본 손실 문제를 극복할 수 있는 대안으로서 기계학습 기반 지수의 추정의 안정성과 시의성을 검토한다. 이를 통해 국내 월세 시장의 구조적 특성과 가격 변동성에 대한 보다 정확한 이해에 기여하고자 하며 나아가 정책 및 경제적 의사결정에 필요한 근거 자료를 제공하고, 국내 월세 시장 연구에 객관적이고 시의성 있는 분석 기반을 제시하는 것을 궁극적인 목표로 한다.
Ⅱ. 이론적 배경 및 선행연구 검토
최근 국내 주택 임대차 시장에서는 전세의 월세화 현상이 두드러지게 관찰되고 있다. 서울 아파트 전·월세 시장에서 전세 계약 비중은 2011년 기준 81.54%에서 2024년 56.56%까지 하락하였다. 반면, 같은 기간 월세 계약 비중은 3.88%에서 8.83%로 상승하였고, 준월세 비중은 3.13%에서 13.63%로 크게 확대되었다. 이러한 변화는 아파트 시장에서 전세보다 월세에 대한 수요가 상대적으로 증가하고 있음을 시사한다(<표 1>).
주 : 원혜진 외(2020)에 따라 보증금/월세 배율을 기준으로 30배 이하인 경우 월세시장, 30배 초과 300배 이하인 경우 준월세 시장, 300배 초과인 경우 준전세시장, 보증금만 있는 경우를 전세시장으로 구분하였다.
‘전세의 월세화’ 배경으로는 먼저, 빌라 시장에서 발생한 대규모 전세 사기가 사회 문제로 대두되며 전세 제도에 대한 불신과 기피가 확산된 점을 들 수 있다. 또한 전세 대출 문턱이 높아지면서 전세 수요가 월세 시장으로 일부 전이된 점도 주요한 원인이다. 한편 2020년 및 2021년에 도입된 주택임대차 보호법 및 부동산 거래신고 등에 관한 법률(일명 ‘임대차 3법’) 역시 신규 전세가격 상승을 야기하여 상대적으로 월세 시장 수요가 높아진 것으로 판단된다.
국제적 측면에서는 코로나19 이후 전 세계적으로 월세 급등 현상이 보고되었다(Kuk et al., 2021). 대부분의 국가에서 사회적 거리두기 조치가 시행되면서, 소비자들의 주택 공간에 대한 수요 증가가 포착되었다. 또한 팬데믹 종식 이후의 고금리 기조는 비용 증가로 주택 건설을 더욱 위축시키는 결과를 초래하였으며, 제한된 부동산 공급 속에서 수요 증가가 월세 상승을 가속화시키는 주요 요인으로 작용하였다(The Economist, 2024).
월세 가격 상승이 지속되는 상황에서, 공공과 민간 통계 간의 변동 추이가 과도하게 저평가되어 상반된 결과를 보이면서 논란이 지속되고 있다. 특히 조사·평가 기반 지수가 과도하게 저평가된 변동 추이를 보인다는 지적이 제기되면서, 주택가격동향조사에 대한 사회적 관심이 집중되고 있으며 보다 신속하게 시장 가격을 반영할 수 있는 실거래가 기반 지수에 대한 요구도 커지고 있다(이창무, 2024).
특히 국내 월세가격지수는 실거래가격 기반 지수가 부재하다. 현재 국내에서 작성·발표되는 주요 월세지수로는 한국부동산원의 월세지수,1) KB국민은행이 작성·발표하는 국민은행 주택가격지수,2) 그리고 한국은행이 소비자물가지수에 포함하여 발표하는 집세지수(월세지수)가 있다. 2019년 1월부터 2023년 6월까지 KREB 월세지수는 4.4%, KB 월세지수는 18.4%, 소비자물가지수(집세지수) 내 월세지수3)는 3.0% 증가하는데 그쳐, 조사·평가 가격 기반과 지수의 현실화에 대한 검토와 더불어 실거래가 기반 지수와의 비교검토가 요구되고 있다(Kim, 2024).
국내의 월세가격은 해외의 일반적인 사례와 달리 보증금 제도의 특수성으로 인해 복잡한 구조를 갖는다. 대부분의 국가에서는 일정 비율의 월세 보증금을 에스크로 계좌에 보관할 의무가 있으며, 이는 미납 임대료를 보전하는 역할을 한다. 그러나 한국의 월세시장에서는 보증금과 월세의 배율 관계에 따라 다양한 하위시장이 형성된다. 비아파트 시장과 달리 아파트 시장은 보증금 규모가 높은 준전세의 비중이 크고, 보증금이 매매가 또는 전세가의 영향을 크게 받는 특징을 보인다(송영선 외, 2022; 이창무, 2012). 즉, 임대료 지수는 전세지수와 매매지수와 달리 월세와 보증금 두 금액의 지불방법의 조합에 의하여 임대료의 수준이 결정되므로, 보증금 비중이 서로 다른 임대료 간 변동분을 측정하기 위해서는 동일한 계약형태로 환산한 후 가격변화율을 산출하는 것이 필수적이다.
월세가격지수에 관한 기존 선행연구로 지수의 작성 방식과 가중치의 결정, 월세지수 산정을 위한 월세시장 세분화 등의 연구가 진행되어 왔다. 월세 지수를 산정하는 방법으로 반복매매모형에 대한 연구가 주를 이루었다. 반복매매모형은 같은 주택이 두 번 이상 거래되었을 경우 거래가격의 변동 비율을 통해 지수를 작성하는 방법이다. 이는 Bailey et al.(1963)을 시작으로, Case (1986), Case and Shiller(1987), Shiller(1991), Goetzmann(1992) 등에 의해 발전되어 왔다. 반복매매지수는 지수산정을 위해 많은 반복적으로 거래된 주택의 거래시점과 가격에 대한 정보만 있으면 지수를 산정할 수 있다는 장점이 있다(이창무 외, 2013).
이창무 외(2013)는 반복매매모형의 경우 거래 량이 더욱 적은 주택 하부시장의 경우 반복 거래 표본을 확보하기 어려운 점으로 인하여 통계적인 신뢰도가 확보되지 못하는 문제를 지적하였다. 이러한 제약을 보완하기 위하여, 이상치의 영향 을 줄일 수 있는 방안으로 분위회귀(quantile regression)를 적용하여 OLS(ordinary least squares) 기반 지수산정방식과 비교하였다. 분석 결과, 분위회귀를 이용하여 지수를 산정할 경우, 전 체적으로 변동성이 둔화되는 경향성이 나타나 적 정 수준의 표본수가 요구되면서도 통계적 신뢰도 를 크게 훼손하지 않고 지수의 불안정성을 완화할 수 있는 대안이라고 판단하였다.
최성호 외(2011)는 반복매매모형을 활용하여 비율월세와 순수월세의 차이 및 가중치의 부여방식에 따른 차이를 실증적으로 검토하였다. 월세지수를 산정할 경우, 비율 월세 방식이 실질적으로 보증금의 크기에 따른 가격변화를 반영하므로 시장 변화를 보다 잘 반영하지만 보증금의 기회비용을 일정 부분을 반영할 수 없는 한계를 지니게 되어 완전월세를 활용하는 방식이 이론적으로 타당하다고 제시하였다.
류강민 외(2009)는 반복매매모형 지수를 중심으로 모든 주택에 동일한 가중치를 주는 동일가중평균법과 대형 또는 고급주택의 가격변동에 민감하게 반응하여 특정 지역 주택 시장의 총 자산 변화를 포착할 수 있는 가치가중평균법을 비교 검토하였다. 만약 가치 기준 가중평균으로 계산한 지수가 더 가파르게 상승했다면, 이는 고가 주택의 가격 상승률이 저가 주택보다 상대적으로 더 컸다고 해석할 수 있는 점을 제시하였다.
원혜진 외 (2020)는 월세 대비 보증금 배율을 기준으로 표준월세, 준월세, 준전세 등으로 구분하고 각 구간별로 대표 월세를 선정하여 하위시장별 지수를 산출하였다. 기존 연구에서는 전월세전환율을 일괄적으로 적용하여 보증금을 완전월세로 환산하는 방식을 활용하였으나, 이러한 방식은 보증금 배율에 따른 구체적인 하부시장만의 변동률이 반영되지 않아 실제 월세시장의 체감도를 왜곡할 수 있는 점을 지적하였다. 보증부 월세 시장에서 보증금 비중에 따라 임대료 변동 추이가 상이하게 나타날 가능성을 고려하여 보증금 비중별로 세분화된 임대료지수를 개발하였다.
한편, 반복매매모형 지수는 새로운 반복 매매 사례가 추가될수록 과거의 지수가 달라지는 문제로 부터 자유롭지 못하다. 새로 추가된 매매 쌍이 과 거 시점의 가격 추정치에도 영향을 미치기 때문 에, 지수가 과거 값까지 함께 수정되는 현상이 발 생할 수 있다. Clapham et al.(2006)은 반복매매 사례가 추가될 때마다 과거의 지수값이 하락하는 현상을 지적하였다. 이용만(2007)은 이러한 현상 을 제어하기 위하여 연쇄지수방식(chain index method)을 활용하여 시간변동계수 모형 기반 지 수를 작성하고 이를 반복매매모형 지수와 비교하 였다.
기존 연구에서 검토한 반복매매모형 기반 지수는 몇 가지 한계를 지닌다. 첫째, 전체 자료 중 반복 거래된 사례만을 활용하기 때문에 전체 시장을 대표하는 데 한계가 있으며, 이로 인해 자료의 비효율성이 발생할 가능성이 있다. 둘째, 반복 거래된 주택이 특정 유형이나 지역에 편중될 경우, 표본의 대표성이 저하되는 편의 문제가 발생할 수 있다. 셋째, 반복매매모형은 거래 간 가격 변동의 분산이 일정하지 않은 이분산(heteroskedasticity) 문제를 내포할 수 있으며, 이는 추정 결과의 신뢰성을 저하시킬 수 있다(류강민 외, 2009; 이창무·배익민, 2008; Case and Shiller, 1987; Goetzmann, 1992; Goetzmann and Peng, 2002; Peng, 2002).
기계학습은 데이터 패턴을 토대로 함수 형태를 스스로 파악하는 포착하는 기법으로, 2010년대 이후 발전이 가속화되면서 전통적 통계 모형과 비교하여 높은 추정 성능을 달성할 수 있음이 보고되었다. 특히 변수간의 비선형 관계와 상호작용 효과의 추적을 통해 변동모수 모형의 주요한 한계였던 함수 형태 오지정 문제를 완화하는 방식으로 발전하고 있다.
기계학습은 주택시장, 특히 주택가격 추정 모형(automated valuation model, AVM) 분야에서 높은 성과를 보이고 있으며, 이미 프롭테크 분야에서도 상용화가 이루어지고 있다. 국내에서 기계학습을 활용해 주택가격을 추정·예측한 대표적 연구로는 김이환 외(2022), 김진석(2024), 민성욱(2017), 배성완·유정석(2018), 그리고 전해정·양혜선(2019)의 연구가 있다.
민성욱(2017)은 서울시 아파트 가격과 거시경제 변수를 활용하여 SVM(support vector machine), RF(random forest), 다층 퍼셉트론 등 머신러닝 기법을 적용하여 주택가격을 예측하였다. 분석 결과, 다층 퍼셉트론 모형이 다른 모델에 비해 가장 우수한 예측 성능을 보이는 것으로 나타났다.
배성완·유정석(2018)은 부동산 가격지수 예측에 SVM, RF, GBM(gradient boosting model), 심층신경망, LSTM(long short term memory) 등 머신러닝기법과 함께, 시계열 모형을 적용하여 매매실거래가격지수를 예측하고 모형간 예측력을 비교하였다.
전해정·양혜선(2019)은 거시경제 변수와 아파트 실거래가격지수를 활용하여 딥러닝의 Simple RNN(recurrent neural network), LSTM, GRU(gated recurrent unit) 모형을 이용해 주택가격 예측력을 비교·분석하였다. 분석 결과, 학습 데이터는 GRU 모형이, 검증 데이터는 RNN 모형의 예측력이 높다고 하였고, 모형 성능의 정확도는 GRU 모형과 RNN 모형의 예측력이 우수하다고 보고하였다.
김이환 외(2022)는 기존 연구에서 성능이 입증된 RF와 인공신경망(artificial neural network, ANN) 기법 등을 적용하여 주택가격을 추정하고 지역별 시점별 지수를 작성하였다. 이 과정에서 주택 실거래 자료와 개별 주택 정보를 매칭하여 훈련 데이터를 구축하였으며, 모형 성능 측면에서 기계학습 기반 주택가격 추정 모형이 헤도닉 지수보다 높은 설명력과 예측 성능을 보이는 것으로 나타났다. 특히, RF 기반 모형이 가장 우수한 예측 성과를 보였다. 해당 연구에서 제시된 방법론은 반년 단위로 지수를 발표하는 방식으로 인해 실용성이 제한되는 한계를 지닌다. 향후 연구에서는 오버샘플링 기법을 활용한 합성 데이터 생성 및 지수 발표 주기 단축 방안을 검토할 필요가 있다고 제언하였다.
김진석(2024)은 LightGBM과 ANN으로 학습 한 AVM을 기반으로 아파트의 월별 가격을 추정 하고 머신러닝 기반 매매가격지수를 산출하였다. 이를 위해 시가총액 방식의 레스파이레스 지수와 기하평균 방식의 제본스 지수를 산정하고 이를 KB국민은행 및 한국부동산원의 기존 매매가격지 수와 비교하였다. ANN 기반 지수는 LightGBM 기반 지수에 비해 소규모 지역에서도 매끄러운 흐 름을 나타냈지만 시장 침체기에 변동을 반영하지 못하여 일시적인 평활화 경향도 포착되었다. 반면 LightGBM기반 지수는 거래량이 부족한 시기에 비교적 매끄럽지 않은 흐름을 보였으나 하락시장 의 가격을 더 민감하게 반영하고 있음을 제시하였 다. 두 모형의 평균으로서 추정 정확도가 가장 높았 던 Ensemble 모형 기반 지수는 시장 침체기의 평활화 경향이 덜하면서, 거래 표본이 부족한 시기에 도 자연스럽게 변동하는 경향을 보였다.
기계학습을 활용하여 주택 매매가격을 추정하는 연구는 비교적 활발하나, 국내 다양한 하위시장으로 이루어져 있는 임대차 시장의 복잡성을 반영한 전월세 추정 모형과 그에 기반한 지수 연구는 전무하다. 본 연구에서는 월세가격의 구조적 특성을 반영한 기계학습 기반의 월세가격 추정 모형을 구축하고, 이를 바탕으로 월세지수를 산정한 후, 타 기관이 작성한 월세지수와의 비교를 통해 기존 지수 작성 방법론의 타당성과 한계를 종합적으로 검토하고자 한다.
Ⅲ. 월세가격지수 산정 방법
본 연구는 월세가격지수를 산정하기 위해 2011년 1월부터 2024년 12월까지 168개월 동안 발생한 신규 보증부 월세 계약을 중심으로 면적당 순수 임대료의 기초통계를 살펴보고 반복매매지수와 기계학습 기반지수를 작성하여 타 기관에서 작성된 조사·평가 기반 월세지수와 비교하였다.
본 연구에서는 K-Apt 공동주택 관리정보서비스에서 정보 공개 의무단지4)에서 거래된 월세 거래 건을 대상으로 한다. 이는 거래량이 적은 소규모 아파트에서 발생할 수 있는 가격 왜곡과 이상치를 배제하고, 보다 신뢰성 있는 월세 가격지수를 산출하기 위함이다. 최종적으로 서울에 소재하는 총 2,160개 아파트 단지의 1,627,871세대5)를 대상으로 하였으며, 2011년 1월 실거래가격이 공개된 이후 최근까지 168개월(14개년도) 동안 발생한 신규 월세 계약 건수는 409,730건6)으로 집계되었다.
월세 시장은 보증금과 월세액이 병존하는 이원적 가격구조를 가지므로, 월세가격지수 산정을 위해서는 이를 순수월세로 환산할 수 있는 전월세전환율의 산정이 필요하다. 본 연구에서는 송영선 외(2022)와 원혜진 외(2020) 등의 선행연구와 한국부동산원(2023)의 전월세전환율 산출 방법을 참고하여 전월세전환율을 산출하였다.
전월세 확정일자 신고자료를 활용하여 전세가격과 보증부월세 자료를 병합하고, 동일 시점 기준으로 동일 아파트 단지 내 동일 면적 구간(30~ 60m2, 60~85m2, 85~180m2)에 속하는 경우를 동일 주택으로 가정하여 분류하였다. 이러한 기준에 따라 분류된 개별 주택의 전세가격은 중위값을 기준으로 월세 자료와 병합하여 각 사례별 전월세전환율을 산출하였다. 산정된 개별 전환율의 중위값을 활용하여 최종 전월세전환율을 계산하였다. 매월 산정된 전환율이 안정적이지 않아, 초기 6개월간은 고정된 전환율을 적용하였으며, 이후 기간에 대해서는 직전 6개월간의 자료를 기반으로 이동 평균값을 계산하여 월별 전환율로 확정하였다.
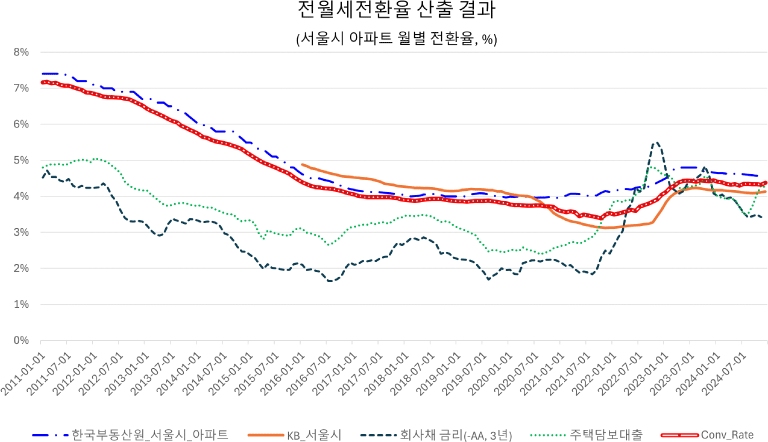
산출된 전월세전환율의 적정성을 타 기관의 전월세전환율 및 주택담보대출금리와 일반적인 시장수익률을 대표하는 회사채(3년, ‒AA) 금리를 함께 비교한 결과는 <그림 1>과 같다. 본 연구에서 산출한 전월세전환율은 2011년 1월 7.2%에서 2017년 상반기 4.0%까지 하락하는 점은 전반적으로 한국부동산원 서울 지역 아파트 전월세전환율과 유사한 추이를 보이는 것으로 나타났다. 해당 기간 전월세전환율은 시장이자율로 대표되는 회사채 금리와 비교하여 2%p에서 3%p 높은 위험프리미엄을 유지해왔다. 2021년 하반기부터는 기준금리 인상의 영향으로 위험프리미엄이 축소되었고 2024년까지 회사채 금리가 높게 유지되었다. 주택담보대출 금리와 회사채 금리의 상승 이후 일정 시차를 두고 전월세전환율이 상승하는 패턴이 관찰되었다. 이는 전월세전환율이 주택 임대차 시장에서 대출금리 및 시장 이자율의 변동을 직접적으로 반영함을 보여준다. 즉, 시장금리의 상승에 따라 전월세전환율 역시 상승 압력을 받게 되었으며, 이는 월세시장에서 임대인의 기대수익률 조정과 월세 선호 증가로 이어지고 있는 것으로 나타난다.
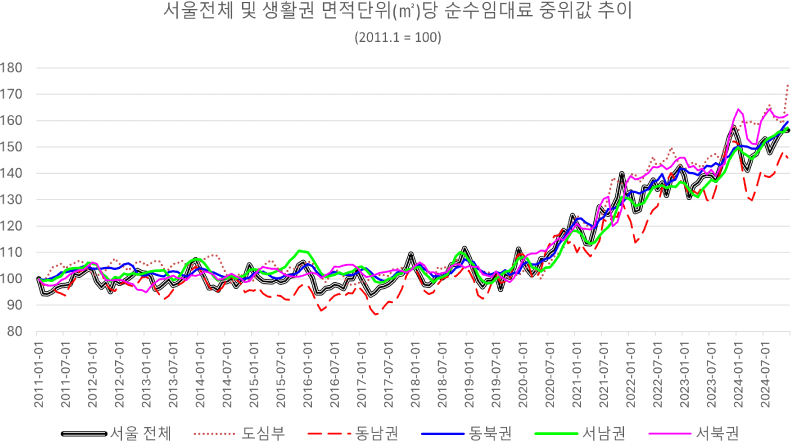
앞서 산출한 전월세전환율을 적용하여 순수 임대료(yearly rent)를 산정하였다. 이를 전용면적으로 나눈 단위면적(m2)당 순수 임대료의 추이는 <표 2>와 같다. 서울시 전체의 2011년 순수 임대료의 평균 및 중위 단위면적당 순수 임대료는 22~25만 원/m2에서 2024년에는 34~38만 원/m2에 근접하는 것을 알 수 있다(<그림 2>). 2011년 상반기부터 2019년 하반기까지 보합세로 나타나지만 2020년 상반기 급격한 상승추세가 나타난다. 2011년 기준 서울시 전체 평균 및 단위면적당 중위값 순수 임대료의 누적 상승률은 약 각각 1.55배와 1.52배인 것으로 파악되었다.
생활권 지수도 서울시 전체추이와 전반적으로 비슷한 추세를 보인다. 이를 월별추이로 보았을 때, 연중 계절성을 띄어 변동성이 매우 크게 나타났다. 생활권별로는 동남권 아파트 월세지수가 가장 낮은 누적 상승률(1.39배)을 보였고, 동북권(1.42배), 서남권(1.48배), 도심부(1.54배), 서북권(1.55배) 순으로 높아졌다. 거래량 측면에서는 거래비율이 높은 동남부권(34.31%)과 동북권(27.76%) 그리고 서남권(23.98%)의 변동성이 서울시 전체에 미치는 영향이 매우 높은 것을 알 수 있다.
실거래 가격을 이용한 부동산 가격 지수 산정, 특히 임대료 산정에 있어서 대표적으로 반복매매모형(Bailey et al., 1963)을 적용할 수 있다. 반복매매지수는 주택의 다양한 특성 정보가 요구되지 않아 적은 비용으로 간편하게 지수 산출이 가능한 장점이 있어 한국 부동산원을 비롯한 다양한 지수 작성기관에서 활용된다.
반복매매모형은 2회 이상 거래된 주택의 거래쌍을 구성하여, 첫번째 거래 시점(f)의 월세가격과 두번째 거래시점(s)의 월세가격의 가격비를 종속변수로 하여 기준시점 대비 t시점의 누적변동률을 나타내는 가격지수를 추정하는 형태로 구성되며 다음 (식 1)과 같이 나타낸다.
여기서 시간더미 D는 t=s인 경우1, t=f 인 경우 =-1, 그 외에는 0의 값을 가지며, 최소제곱법을 통해 추정된 βt는 기준시점 (t=1)을 기준으로 한 t시점의 누적 로그가격변동률을 나타낸다. 따라서 최종적으로 가격지수는 추정된 βt를 다시 지수화하여 (식 2)와 같이 산정할 수 있다.
본 연구에서 반복매매지수의 작성을 위하여 동일주택가정 기반 반복거래쌍을 구성하였다. [주소, 동일 층, 동일 면적]을 이용하였다. <표 3>은 동일주택가정 자료의 수를 나타낸다.
기계학습 기반 가격지수의 산정 과정은 세 가지 단계로 구성된다. 첫째, 시점별 모형이 아닌 전체 기간에 대한 자료를 투입하여 학습한 후, 둘째로, 모든 시점에 대해 모든 아파트 단지에 대하여 면적 유형별 가격을 추정한다. 마지막으로, 추정한 가격에 대해 면적 유형별 세대수를 가중치로 하여 월세지수를 산정한다. (식 3)에 따라 각 시점의 지수는 기준연도 대비 총 자산가치의 변동을 반영한다.
본 연구에서는 선행연구에서 기존 매매가격추정에 있어서 정확도가 높게 도출되었던 트리기반 학습 모형인 그래디언트 부스팅과 인공신경망 모형을 활용하여 각 면적별 가격을 산출하였고, 각 가격지수의 특성을 검토한 후 이를 가중평균한 앙상블 가격(ensemble price)를 산출하였다.
GBM과 ANN의 투입변수는 <표 4>와 같다. 타깃 변수는 거래 가격(만 원)이다. 기존 연구와 달리 면적당 가격을 사용하지 않은 이유는 개별 면적 유형에 대해 세대수를 곱하는 시가총액 방식으로 산정하기에 면적당 가격보다 거래가격이 산출 과정상 더 자연스럽기 때문이다. 면적 변수를 모델에 별도 투입함으로써 면적에 따른 가격 차이를 효과적으로 통제할 수 있다.
| 구분 | 단위 | 예시 | |
|---|---|---|---|
| Target | Pure rent | 만 원 | 2,500 |
| Feature | Floor | 해당 주택 층수 | 5 |
| Area | 전용면적 | m2 | |
| Latitude | x(epsg: 4,326) | 37.5332 | |
| Longitude | y(epsg: 4,326) | 127.2299 | |
| Trade time | Integer | 3 | |
| Households | 세대 | 525 | |
훈련 변수로는 선행연구에서 공간 패턴에 대한 학습의 효율성을 기반으로 아파트 단지의 공간정보를 나타내는 위도와 경도를 투입하였다. 또한, 시점에 대한 정보는 정수 형태의 Trade_Time 변수(0~167)를 투입하여 학습하였다.
그래디언트 부스팅 모형이란 결정 트리를 순차적으로 학습시켜 예측 성능을 향상시키는 기계학습 모형이다. 경사하강법(gradient descent)이란 손실함수의 기울기를 이용해 오차가 최소화되는 방향으로 파라미터를 조정함으로써, 예측값과 실제값 간의 차이를 줄이는 최적화 알고리즘으로, Friedman(2001)이 최초로 제안하였다. 부스팅 모형(boosting model)이란 예측력이 여러개의 약한 모형들을 결합하는 방식으로 강한 예측 모형을 만드는 방식을 말한다. 여기서 약한 모형이란 완전 임의로 예측하는 것보다는 약간 좋은 모형을 의미하고, 강한 모형이란 예측력이 매우 뛰어난 모형을 의미한다. 본 연구에서는 GBM의 고속성과 효율성을 개선한 버전인 LightGBM 모형을 적용하였다.
하이퍼 파라미터 최적화를 위해 Optuna를 활용하였으며 손실함수로는 평균제곱오차(mean squared error, MSE)를 최소화하는 회귀 손실함수(regression)를 적용하였다. 최종 선정된 최적 설정은 다음과 같다: 학습률(learning rate)은 0.1, 최대 깊이(max_depth)는 ‒1, 리프 노드 수(num_leaves)는 511, 리프 노드당 최소 데이터 수(min_data_in_leaf)는 5이다(<표 5>).
ANN 모형은 기계학습 기법의 일종으로, 인간의 신경망의 개념에서 착안하여 알고리즘으로 구성한 방법이다. 모형은 입력층, 은닉층, 출력층으로 구성되며, 입력된 데이터는 각 층의 노드에서 가중치가 적용된 후, 비선형 활성화 함수를 통과하여 다음 층으로 전달된다. 최종 출력층에서의 예측값과 실제 거래가격 간의 차이를 기반으로 손실(loss)이 계산된다. 학습이 진행되는 동안, 모형의 가중치는 전체 손실을 최소화하는 방향으로 업데이트되며, 데이터의 변수 간 비선형적 관계가 학습된다.
본 ANN 모형에서는 훈련 데이터의 손실함수로 MSE를 적용하였으며, 검증 데이터에 대한 손실함수로 평균절대백분오차(mean absolute percentage error, MAPE)를 적용하였다. 은닉층의 활성화 함수는 ReLu를 적용하였다(<표 6>).
기계학습 방법론의 경우 과적합(over-fitting) 문제, 즉 학습 모형이 훈련 데이터에 지나치게 맞추어져 일반화 능력이 떨어지는 현상이 발생할 수 있다. 이는 모델이 데이터의 비선형 패턴뿐만 아니라 이상치까지 학습하기 때문이다. 이러한 과적합 현상을 방지하기 위하여 본 연구에서는 ANN 모형에 대해서 일부 은닉층에서 드롭아웃(dropout) 기법을 적용하여, 특정 노드를 랜덤하게 제거함으로써 모델이 특정한 특징에 과도하게 의존하는 것을 방지하였다. 또한, LightGBM 모형과 ANN 모형 모두 훈련 표본 중 일부(20%)를 검증 데이터로 사용하였으며 검증 성능을 모니터링하여 30회 연속 성능 개선이 없을 경우 학습을 중단하는 조기 종료(early stopping) 기법을 적용하여 학습과정에서 모델이 훈련 데이터에 과대 적합되지 않도록 하였다.
Ⅳ. 지수 작성 결과
서울시 전체와 생활권역별 반복매매지수를 산정하였다. 일반적인 회귀모형에서는 추정계수나 모형의 설명력(R-squared) 등을 활용하여 모형의 유의성을 평가하지만, 반복매매모형의 지수 추정 결과에서 나타나는 유의확률은 기준 시점 대비 가격 변화의 유의성을 보여주는 데 그치며, 설명력 또한 일정 부분 유의확률에 비례하여 높아지는 경향이 있어 지수 추정 모형의 통계적 검증 지표로서 충분히 활용되기 어렵다(류강민·송기욱 2021; 송영선 외, 2022). 대신에 통계적 신뢰도를 비교, 검증하기 위한 지표로 평균 표준오차를 활용할 수 있다. 본 연구에서 평균 표준오차는 서울 전체 모형은 0.02, 생활권별 모형은 0.0056에서 0.0062로, 지수 모형의 설명력이 우수하다고 판단할 수 있는 기준으로 제시된 0.02보다 같거나 모두 낮은 수준이다. 따라서 본 연구에서 산정된 지수는 모두 통계적 신뢰도를 충분히 확보하였다고 판단하였다.
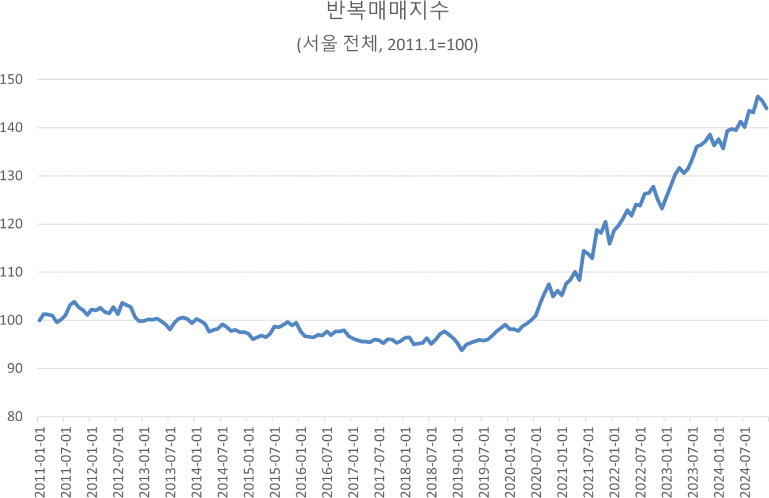
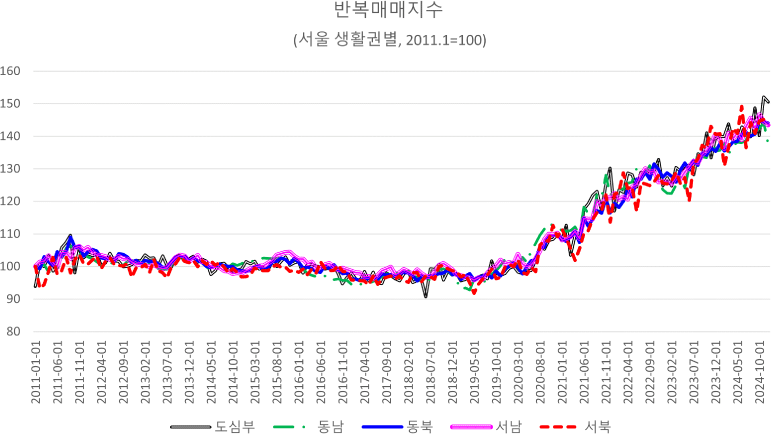
<그림 3>과 <그림 4>는 각각 반복매매모형으로 산정한 서울시 전체 월세지수와 생활권별 월세지수를 나타낸다. 중위값 추이와 마찬가지로 2019년 하반기까지 100을 중심으로 보합세를 유지하다가, 2020년 상반기부터 2024년 하반기까지 약 150까지 상승하는 형태를 보여준다. 생활권별 지수도 서울시 전체 지수 추이와 유사하며, 생활권별 중위값 추이와 같이 도심부, 서남권, 서북권의 누적상승률이 높았고, 동남권이 가장 낮은 상승률을 나타냈다. 서울시 전체 지수와 생활권별 지수 모두 계절성과 같은 노이즈가 반영되어 지수의 변동성이 크게 나타났으며, 전반적으로 불안정한 양상을 보이고 있다(<표 7>).
월세가격추정 모형 중 인공신경망 모형의 MAPE 값은 8.5114%, 그래디언트 부스팅 모형은 8.2434%로 준수한 예측 성능을 나타냈다. 앞서 서술한 바와 같이, 원 데이터인 확정일자 자료에 공공임대주택 등의 전월세 계약 정보도 일부 포함되고 있음을 고려할 때, 별도의 산정 기준에 따라 책정된 임대료를 식별하거나 해당 임대계약에 공공 개입이 있었는지 여부, 특수관계인등의 계약 여부를 명확히 판단할 수 있는 알고리즘이 향후 적용된다면, 추정 성능이 추가적으로 향상될 수 있을 것으로 판단된다.
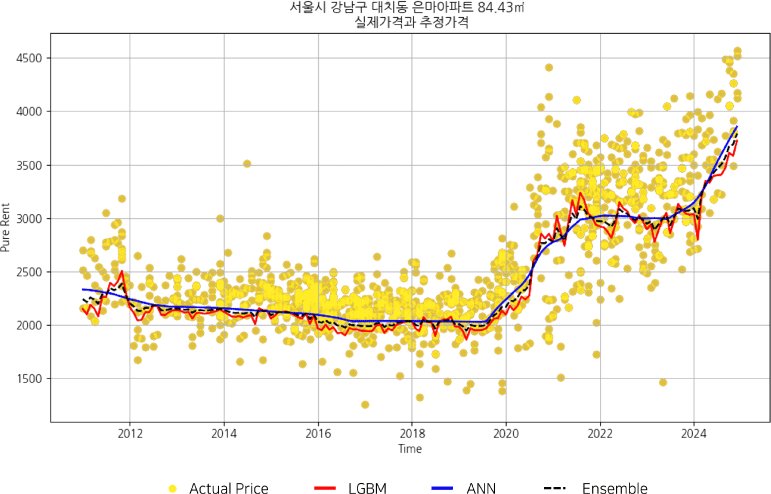
먼저 서울시 소재 아파트의 개별 면적 유형에 대해 ANN 모형과 GBM 모형 기반 월별 월세가격을 각각 추정한 후, 두 결과를 가중평균한 가격(ensemble price)을 산출하였다. 이러한 과정을 구체적으로 서술하기 위해 월세 거래가 가장 많은 대단지 중 하나인 서울시 강남구에 소재한 은마아파트를 사례로 제시하였다. 은마아파트는 총 4,424세대로 구성되어 있으며, 이 중 약 39.6%에 해당하는 1,750세대(전용면적 84.43m2 사례)를 대상으로 실제 월세가격과 각 모형에 기반한 추정가격을 비교한 결과는 <그림 5>에 제시되어 있다.
추정 결과, 2011년 1월 기준 실제 순수임대료(연세) 가격은 2,300만 원에서 2024년 12월 3,700만 원까지 상승하는 형태를 보였다. ANN 모형 기반 지수는 장기적인 가격 추세를 부드러운 곡선 형태로 예측하는 특성을 가지는 반면, GBM 모형 기반 지수는 단기적인 변동성을 보다 정밀하게 반영하는 것으로 나타났다. 이러한 차이를 고려하여 산출한 Ensemble 가격은 두 모형의 특성을 중화하는 역할을 하며, 실거래가의 추세를 균형감 있게 반영하는 것으로 분석되었다.
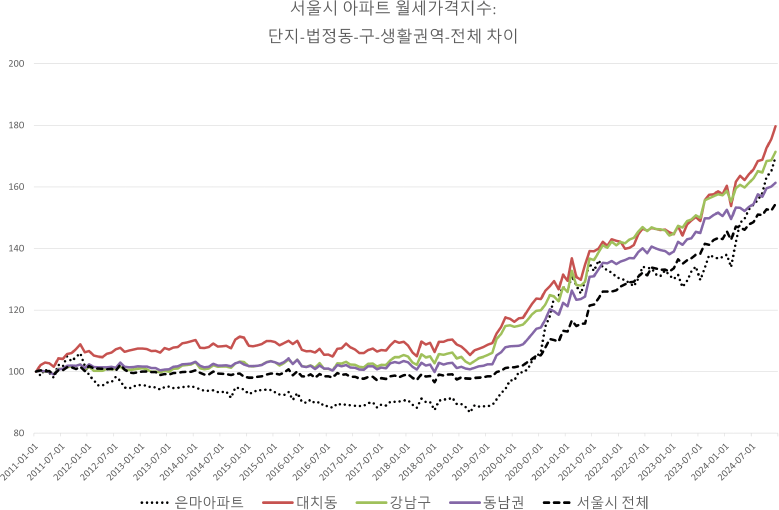
아울러 <그림 6>에서는 개별 아파트 단지, 법정동, 자치구, 생활권역 및 서울시 전체의 월세지수를 비교하여 지역적 차이를 검토하였다. 본 연구에서 예시로 제시된 은마아파트는 법정동으로는 대치동에 속하며, 자치구 단위에서는 강남구, 생활권역으로는 동남권에 포함되는 대표적인 대단지이다. 본 연구의 분석 결과, 은마아파트의 월세지수는 상위 공간 범위의 월세지수와 비교할 때 지속적인 하락 추세를 보이는 것으로 나타났다. 이는 개별 아파트 단지가 상위 지역 지수에 포함되면서도 자체적인 가격 변동성을 따를 수 있음을 시사한다. 다시 말해, 지역 단위의 가격 흐름이 반드시 개별 단지의 가격 변동성과 동일한 방향성을 가지지 않으며, 특정 아파트 단지는 독자적인 월세 시장을 형성할 수 있음을 의미한다.
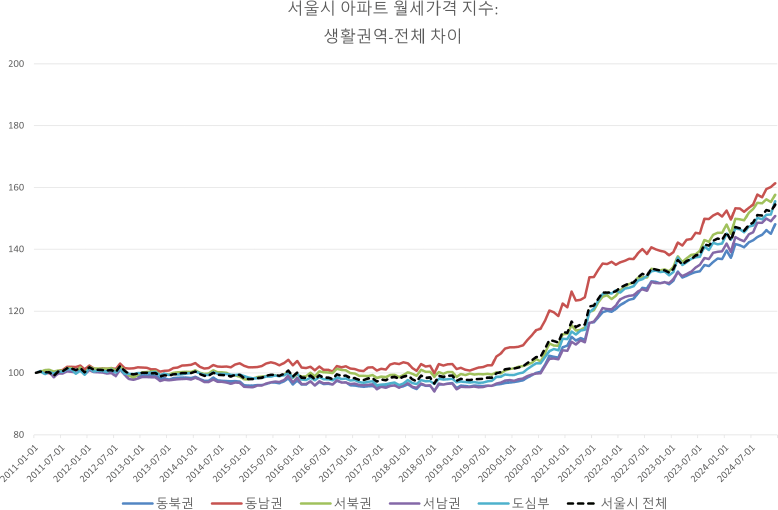
한편, <그림 7>에서는 서울시 생활권역별 월세지수 변화를 비교하였다. 중위값 추세와 반복매매지수에서는 동남권이 가장 낮은 누적 상승률을 보인 반면, 기계학습 기반 가격지수에서는 동남권이 가장 높은 누적 상승률을 보였다. 이러한 차이는 중위값 추세와 반복매매지수는 제한된 표본을 기반으로 가격 변화율을 추정하는 반면, 기계학습 모형은 전체 기간동안의 추정가격을 기반으로 하기 때문에 관측 기간의 모든 주택의 잠재가격을 포함하기 때문에 발생하는 것으로 판단된다.
<그림 8>은 본 연구에서 작성한 실거래가 기반 지수와 타 기관에서 작성한 조사평가기반 월세지수의 2011년 1월부터 2024년 12월까지의 추이를 한 그래프에 나타낸 것이다. 모든 지수가 보합세 또는 소폭 하락하다가 2019년부터 상승추세로 전환한 것을 볼 수 있다. KB 월세지수의 경우 2015년 12월부터, KREB 월세지수의 경우 2015년 6월부터 자료를 제공하여, 2016년 1월 대비 2024년 12월까지의 누적 상승률을 산출하여 비교하였다. 가장 높은 상승률을 보인 지수는 GBM 월세지수(159.03)로, 2016년 대비 약 1.59배 상승한 것으로 나타났다. ANN 월세지수도 유사하지만 소폭 낮은 상승률(1.50배)을 보였으며, GBM과 ANN을 가중평균한 Ensemble지수는 1.54배 상승한 것으로 나타났다. 반복매매모형은 기계학습기반 모형보다 약 10%p 낮은 147.56으로 산출되었다. KB 월세지수는 1.325배, KREB 월세는 1.057배로 가장 낮은 누적 상승률을 보이며 지수 중에서도 가장 완만하게 증가한 것으로 나타났다.
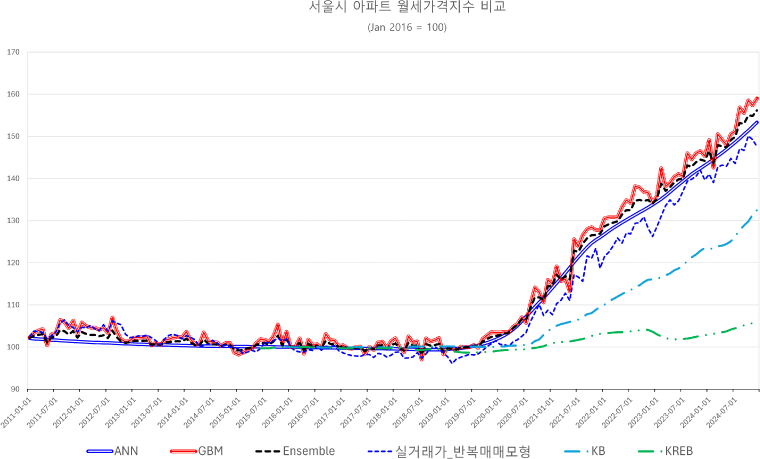
실거래가 자료가 존재하는 전체기간의 변동성과 안정성을 평가하기 위한 지표로 변동성 계수7) 를 산출하여 비교하였다(<표 8>). 산출 결과, GBM 기반 월세지수(7.591)가 변동성계수가 가장 높았으며, 반복매매지수(5.659)가 그 다음으로 변동성이 높게 산출되었다. 가장 변동성이 작은 지수로는 ANN 기반 월세지수(1.481)와 KB 월세지수(1.262)가 가장 안정적이고 부드러운 변화를 보였다.
기계학습 기반 지수의 변동성 계수가 적게는 1.481, 많게는 7.591에 이르는 것은 각 기계학습 모형의 학습 방식 차이에서 기인하는 것으로 판단된다. GBM 기반 월세지수는 여러개의 결정 트리(decision tree)를 결합한 부스팅 알고리즘으로, 성능이 낮은 약한 학습기(weak learner)를 결합시켜 전체 예측 성능을 향상시키는 방식이다. 결정 트리 알고리즘은 입력 공간을 분할하여 오차를 최소화하는 최적의 분기점(best split point)을 찾아내고, 각 구간에서 출력을 일정하게 유지하기 때문에 추정치는 계단 형태를 띤다. 이러한 트리들이 반복적으로 합산되는 과정에서도 예측값은 여러 개의 계단 구조가 누적되는 형태를 보이며, 결과적으로 해당 모형으로 추정된 지수는 상대적으로 변동에 민감한 특성을 나타낸다.
반면, ANN 기반 모형은 인공 뉴런과 다층 퍼셉트론(multi-layer perceptron) 구조를 활용하는 대표적인 비선형 함수 근사 모델로, 출력값과 실제값 간의 오차 함수를 손실 함수로 정의하고 이를 미분한 기울기 정보를 활용하여 가중치를 반복적으로 갱신하는 방식으로 학습이 진행된다. 이 과정에서 활성화 함수는 출력이 입력에 대해 연속적이며 미분 가능한 형태를 유지해야 하며, 이를 통해 학습의 수렴성과 안정성이 확보된다. 이러한 구조적 특성으로 인해 신경망의 출력은 매 반복마다 연속적인 방식으로 조정되며, 결과적으로 예측값은 비교적 부드러운 연속함수 형태로 나타나는 경향이 있다.8)
한편, 기계학습 기반 지수는 학습과정에서 사용되는 학습률, 정규화 계수, 초기 가중치 등과 같은 패러미터와 모델 설정에 따라 결과가 민감하게 변할 수 있다는 점이 근본적인 한계로 제시된다. 이는 동일한 모델을 반복 실행하더라도 미세한 차이가 발생할 수 있음을 의미하며, 예측의 재현성 확보를 위해 신중한 패러미터 튜닝과 검증 과정이 필수적이다.
기계학습가격 기반 가격지수는 본질적으로 훈련 반복이나 파라미터 설정에 따라 결과가 미세하게 달라지는 특성이 있다. 따라서 실제 적용 시에는 모델 및 하이퍼 파라미터를 고정하고 난수 시드 등을 제어하여 동일 조건에서 미세한 변화에 얼마나 민감한지 평가하여야 한다. 이에 가격지수의 적정성에 있어서 가장 중요한 요소 중 하나인 추정의 안정성을 검토하였다.
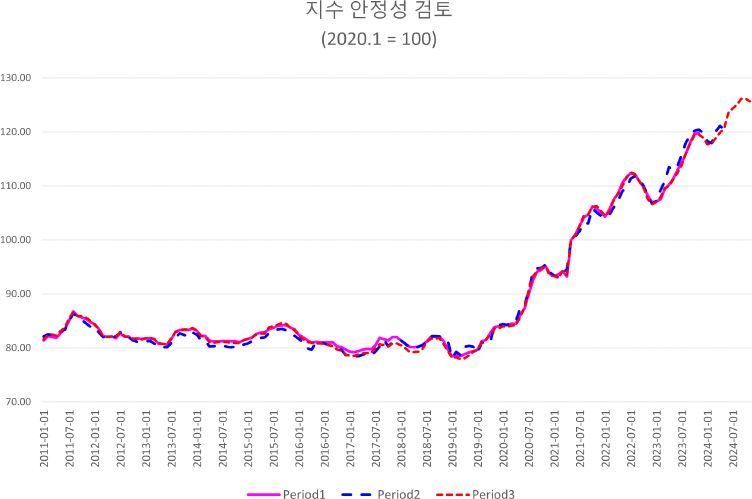
기계학습 기반 지수의 안정성을 분석하기 위하여, 2011년 1월부터 2023년 12월까지의 거래 데이터를 이용해 지수를 산정하고, 이를 ‘초기 지수’로 정의하였다. 이후 2024년 6월까지 확보된 추가 6개월간의 거래 데이터를 반영하여 다시 산정한 지수를 ‘2차 지수’, 2024년 12월까지 확보된 또 다른 6개월치 데이터를 반영하여 산정한 지수를 ‘3차 지수’로 구분하였다. 새롭게 작성한 구간에서 과거 구간의 지수 값이 어떻게 달라졌는지 절대 차이9)와 비율 차이10) 등을 검토하였다. (<그림 9>).
평균 절대 차이는 최초 지수와 2차 지수가 0.26, 2차 지수와 3차 지수는 ‒0.09로 나타났으며, 최초 지수와 2차 지수의 상대적 차이의 평균은 0.32%, 2차 지수와 3차 지수의 상대적인 차이는 평균 ‒0.13%로 나타나 그 결과가 1% 미만 수준으로 안정적으로 나타났다(<부록>). 그러나 일부 구간에서 최대 절대 차이가 1.9~3.4 지수 포인트, 최대 상대차이가 1.9%~3.0%까지 차이남에 따라 지수 산정 정책에 따라 연쇄 가중 방식의 활용하거나 모형 자체에서 랜덤성을 통제하는 방법이 향후 고려될 필요가 있다. 구간별 하이퍼 패러미터의 차이가 발생한다면 수시, 정기적으로 패러미터의 조합을 업데이트 할 필요성도 제기된다(김진석, 2024).
기계학습 기반 지수(ensemble 지수)와 조사·평가 기반 지수인 한국부동산원 월세가격지수 간의 선후행 관계 및 차이를 분석하기 위하여, 전체 기간과 시장 국면별(상승기, 하락기)로 나누어 검토하였다. 한편, KREB 지수의 최초 작성 시점이 2015년 6월임을 고려하여, 전체 분석 기간은 2015년 6월부터 2024년 12월까지로 설정하였으며, 기준 시점은 2016년 1월을 100으로 설정하였다. 상승 시장은 2019년 1월부터 2022년 7월까지, 하락 시장은 2022년 8월부터 2023년 4월까지로 구분하였다.
우선, 로그 차분 자료를 바탕으로 교차 상관 분석(cross correlation analysis)을 실시한 결과는 <표 9>와 같다. 전체 기간 동안 두 지수 간의 교차 상관 계수는 시차(lag) ‒2~‒3 시점에서 0.5864로, 비교적 높은 양(+)의 상관관계를 보였다. 이는 KREB 지수가 약 2~3개월의 시차를 두고 기계학습 기반 지수와 유사한 방향으로 움직이는 경향이 있음을 보여준다.
| Lag | Lead | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | |
| 전체기간 | 0.3538 | 0.5864 | 0.5820 | 0.5170 | 0.3945 | 0.2400 | 0.0732 | 0.0163 | 0.0498 |
또한, 상승기와 하락기에서 지수간의 차이가 비대칭적으로 나타나는지를 확인하기 위해, KREB 지수에서 기계학습 기반 지수를 뺀 후 그 값을 다시 기계학습 기반 지수로 나눈 비율을 산출하여 비교하였다. 분석 결과, 전체 기간 두 지수 간 평균 차이는 약 9.50%로 나타났다(<표 10>). 시장 국면별로 살펴보면, 상승기에는 9.25%의 차이를 보인 반면, 하락기에는 22.08%로 차이가 크게 확대되었다. 이는 상승기에서도 차이가 존재하지만, 특히 하락기에서 KREB 지수가 기계학습 기반 지수에 비해 상대적으로 더 완만하게 조정되는 경향이 있다는 점을 보여준다. 이러한 결과는 선행연구의 결과(김현영 외, 2018; 박연우·방두완, 2011)와도 일치한다.
| 관측 기간 | 평균 차이 % | t-statistics | p-value | |
|---|---|---|---|---|
| 전체기간 | 2015.6~2024.12 | 9.50 | 8.523 | 0.0000 |
| 상승시장 | 2019.1~2022.7 | 9.25 | 7.442 | 0.0000 |
| 하락시장 | 2022.7~2023.4 | 22.08 | 79.56 | 0.0000 |
V. 결론
본 연구는 국내 월세 시장의 특수성을 체계적으로 반영한 지수 작성 방식을 탐색하고, 실거래가를 활용한 월세지수 개발 가능성을 검토하였다. 이를 위해 실거래가를 기반으로 중위값 추이를 검토하고 반복매매모형 지수와 기계학습 기반지수를 산정하여 타 기관 작성 지수와 비교 검토하였다. 본 연구에서는 기계학습 기반 지수 산출을 위해 그래디언트 부스팅 계열의 LightGBM과 ANN 모형을 적용하였다.
먼저, 순수임대료 기준 전월세확정일자 신고자료의 서울시 전체 중위값 추이를 살펴본 결과, 2011년 1월 대비 2024년 12월에는 약 1.52배 상승한 것으로 나타났다. 같은 자료로 산정한 반복매매지수 역시 이와 비슷한 누적상승률을 보이나 지역이나 거래 공백기 동안 표본 수 감소로 인해 지수의 안정성이 저하될 위험이 있다.
이에 반해 기계학습 기반 월세지수는 거래가 없는 기간과 지역에 대해 안정적으로 지수를 산정할 수 있음이 확인되었다. 구체적으로 GBM 월세지수는 시장의 급격한 변화나 단기적 추세, 계절적 패턴을 포착하는 데 유리한 장점이 관찰되었다. 반면, ANN 월세지수는 연속적인 가중치 업데이트를 통해 출력이 부드럽게 변화함으로써 우수한 평활화 효과를 보였으며, 시장 추세와 계절 패턴을 보다 연속적으로 학습하여 장기적 추세를 파악하는 데 유리한 특성을 지닌다. Ensemble 지수는 이 두 모델의 보완적인 특성을 결합하여 산정한 지수로, 시장 여건이 급격히 변하거나 반대로 완만한 추세가 이어지더라도 어느 한 모델의 편향된 결과에만 의존하지 않으므로 비교적 안정적인 예측을 기대할 수 있다.
기계학습 지수 산정의 안정성을 검토한 결과 최초 산정 지수와 6개월 이후 산정한 2차 지수의 평균 상대 차이는 0.32%, 2차 산정 지수와 3차 산정 지수의 상대적인 차이는 평균 ‒0.13%로 나타나 그 결과가 1% 미만 수준으로 안정적으로 나타났다. 또한, 조사·평가기반 지수가 약 2~3개월의 시차를 두고 기계학습 기반 지수와 유사한 방향으로 움직이는 경향이 있음을 포착하였다. 조사·평가가격에 기반한 KB 및 KREB 월세지수 등은 장기간 축적된 데이터를 바탕으로 안정적인 시장 추세를 파악하는 데 유리하지만, 시장 급변 시 시의성이 낮아지거나 실제 체감하는 월세가격을 반영하지 못함을 시사한다.
근본적으로 기계학습 기반 지수(GBM, ANN, ensemble 등)는 비선형 관계와 다양한 입력 변수를 활용하여 시장 변화에 대한 민감도가 높고 신속한 반응이 가능하지만, 모델 설정에 따른 결과 예측의 재현성 확보를 위한 제도적 방법이 고안될 필요가 있다.
한편, 본 연구에는 다음과 같은 한계가 존재한다. 첫째, 본 연구에서는 추정값과 실제값의 오차항에 대해 기계학습 모형에서 기본적으로 적용되는 MSE를 손실함수로 설정하여 모형의 성능은 평균제곱오차를 최소화하는 방향으로 최적화되었다. 연구에서 활용된 트리 기반 부스팅 모형(GBM)은 전통적인 회귀모형과는 달리 입력변수와 출력변수 간의 함수적 형태를 사전에 가정하지 않는 비모수적 모형(non-parametric model)이며, 인공신경망 모형은 엄격한 의미에서는 모수적 모형(parametric model)이지만, 입력층부터 은닉층을 거쳐 출력층에 이르기까지 비선형 활성화 함수를 통해 매우 유연한 함수 형태를 근사할 수 있다. 이들 모형은 선형성 또는 등분산성과 같은 전통 회귀모형의 강력한 가정을 필요로 하지 않기 때문에, 상대적으로 강인한 예측 성능을 보이는 것으로 알려져 있다(Gelfand, 2015). 그러나 손실함수는 RMSE 외에도 MAPE, Gamma Loss, Huber, Quantile 등의 다양한 형태가 존재하며, 손실함수의 선택에 따라 모형의 추정 결과가 서로 다른 특성과 민감도를 가질 수 있다. 본 연구는 이러한 손실함수 유형에 따른 추정 결과의 차이를 심층적으로 비교·분석하지 못한 한계가 있으며, 향후 연구에서는 손실함수 유형 간의 성능 차이를 체계적으로 분석할 필요가 있다.
둘째, 본 연구에서 산정한 기계학습 기반 월세지수는 총자산 가치의 변동을 반영한다는 가치가중 방식의 지수이다. 이에 반해, 비교 대상인 KB 및 KREB 지수는 Bailey et al.(1963)의 동일가중 반복매매모형에 근거하여 개별 주택의 평균 변동률을 동일한 가중치로 반영한 동일가중 방식에 해당한다. 가치가중 모형은 상대적으로 고가주택의 영향을 더 크게 반영하므로, 보다 정밀한 비교를 위하여 Shiller(1991)가 제안한 가치가중 반복매매모형을 기반 방식의 반복매매지수를 비교하는 것이 타당하며, 향후 다양한 지수 간 비교 분석 시 이러한 가중치 구조의 차이를 고려할 필요가 있다.
마지막으로 앙상블 지수와 관련하여 향후 연구에서는 서로 다른 기계학습 모형에 대한 가중치를 단순히 고정하는 방식에서 나아가, 목표로 하는 예측 정확도 및 시장 상황 변화에 따라 가중치를 동적으로 재조정하는 방안을 구체적으로 탐색할 필요가 있다. 이를 통해 예측 모델의 유연성과 정밀도를 동시에 제고할 수 있으며, 다양한 동적 가중 조정 기법을 적용하여 장·단기 추세 변동에 더욱 효과적으로 대응할 수 있을 것으로 기대된다.
국내 월세 시장은 점차 확대되고 있으나, 기존 월세지수만으로는 시장 상황을 충분히 설명하는 데 한계가 있다. 이에 매매 및 전세시장과 마찬가지로 실거래 기반의 월세지수 개발이 요구되며, 거래 공백기에도 가격 변화를 미시적으로 포착할 수 있는 기계학습 기반 지수는 효과적인 대안이 될 수 있다. 이러한 지수는 인플레이션 측정, 경제정책 수립, 소비자 및 기업의 의사결정 등 다양한 영역에서 활용될 수 있으며, 궁극적으로 국내 월세 시장에 대한 이해를 제고하고 관련 정책의 정교한 설계 및 운용에 기여할 수 있을 것으로 기대된다.